题目内容
已知一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱． 如图所示．（1）若设圆柱底面半径为r，求证：r=R（1-
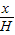）；（2）当x为何值时，圆柱的侧面积最大？并求出这个最大值．
【答案】分析：（1）我们可以画出圆锥的轴截面，将空间问题转化为平面问题，然后根据相似三角形的性质和比例的性质，易得到结论．
（2）由圆柱的侧面积公式，我们易得S侧=2πrx=2πxR（1-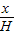
），展开后易得一个关于x的二次函数解析式，根据二次函数的性质易得到其最大值，及对应的x的值．
解答：解：（1）根据已知，如下图所示
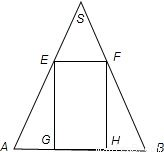
记轴截面为△SAB，EFGH为内接矩形，F在SB上．
则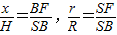
，
则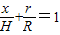
，
r=R（1-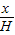
）．（4分）
（2）S侧=2πrx=2πxR（1-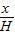
）（6分）
=
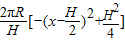（8分）
当x=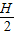
时，ymax=
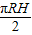（10分）
点评：本题考查的知识点是圆锥的几何特征及圆锥及圆柱的侧面积公式，将空间问题转化为平面问题是解答立体几何题最常用的思路．
（2）由圆柱的侧面积公式，我们易得S侧=2πrx=2πxR（1-
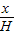），展开后易得一个关于x的二次函数解析式，根据二次函数的性质易得到其最大值，及对应的x的值．解答：解：（1）根据已知，如下图所示
记轴截面为△SAB，EFGH为内接矩形，F在SB上．
则
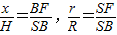，则
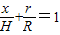，r=R（1-
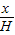）．（4分）（2）S侧=2πrx=2πxR（1-
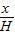）（6分）=
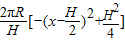（8分）当x=
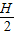时，ymax=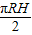（10分）点评：本题考查的知识点是圆锥的几何特征及圆锥及圆柱的侧面积公式，将空间问题转化为平面问题是解答立体几何题最常用的思路．
练习册系列答案
相关题目
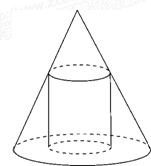已知一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱． 如图所示．
如图，已知一个圆锥的底面半径为R，高为h，在其中有一个高为x的内接圆柱（其中R，h均为常数）．
如图，已知一个圆锥的底面半径为R=1，高为h=2．，一个圆柱的下底面在圆锥的底面上，且圆柱的上底面为圆锥的截面，设圆柱的高为x．