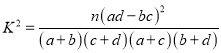题目内容
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 上为减函数,求实数
上为减函数,求实数![]() 的最小值;
的最小值;
(2)若存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)最小值为![]() ;(II)
;(II)![]()
【解析】试题分析: ![]() 在
在![]() 上为减函数,等价于
上为减函数,等价于![]() 在
在![]() 上恒成立,进而转化为
上恒成立,进而转化为![]() ,根据二次函数的性质可得
,根据二次函数的性质可得![]()
![]() 命题“若存在
命题“若存在![]() ,
,![]()
![]() ,使
,使![]() 成立”等价于
成立”等价于
“当![]() 时,有
时,有 ![]() ”, 由
”, 由![]() 易求
易求![]() ,从而问题等价于“当
,从而问题等价于“当![]() 时,有
时,有![]() ”,分
”,分![]()
![]() ,
,![]()
![]() 两种情况讨论:
两种情况讨论:
当![]() 是易求
是易求![]() ,当
,当![]() 时可求得
时可求得![]() 的值域为
的值域为![]() ,再按
,再按![]()
![]() 两种情况讨论即可
两种情况讨论即可
解析:(1)由已知得![]() ,
, ![]()
因![]() 在
在![]() 上为减函数,故
上为减函数,故![]() 在
在![]() 上恒成立。
上恒成立。
所以当![]() 时
时![]() 。
。
又 ,
,
故当![]() 时,即
时,即![]() 时,
时, ![]() .
.
所以![]() ,于是
,于是![]() ,故
,故![]() 的最小值为
的最小值为![]() .
.
(2)命题“若存在![]() ,
,![]()
![]() ,使
,使![]() 成立”等价于
成立”等价于
“当![]() 时,”
时,” ![]() ”,
”,
由(1),当![]() 时,
时, ![]() ,
, ![]()
![]() .
.
问题等价于:“当![]() 时,有
时,有![]() ”.
”.
当![]() ,由(1),
,由(1),![]() 在
在![]() 为减函数,
为减函数,
则![]() ,故
,故![]() .
.
当![]() 时,由于
时,由于![]() 在
在![]() 上的值域为
上的值域为![]()
(i)![]() ,即
,即![]() ,
, ![]() 在
在![]() 恒成立,故
恒成立,故![]() 在
在![]() 上为增函数,
上为增函数,
于是, ![]() ,矛盾。
,矛盾。
(ii)![]() ,即
,即![]() ,由
,由![]() 的单调性和值域知,
的单调性和值域知,
存在唯一![]() ,使
,使![]() ,且满足:
,且满足:
当![]() 时,
时, ![]() ,
, ![]() 为减函数;当
为减函数;当![]() 时,
时, ![]() ,
, ![]() 为增函数;
为增函数;
所以, ![]() ,
, ![]()
所以, ![]() ,与
,与![]() 矛盾。
矛盾。
综上得![]()

练习册系列答案
相关题目