题目内容
【题目】已知向量 ![]()
(1)求函数f(x)的解析式,并求函数f(x)的单调增区间;
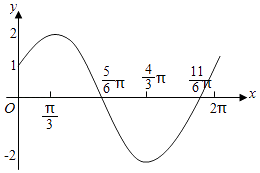
(2)画出函数f(x)在[0,2π]上的图象.
【答案】
(1)解: ![]()
![]() =
= ![]() ,
,
由2kπ﹣ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,解得2kπ﹣
,k∈Z,解得2kπ﹣ ![]() ≤x≤2kπ+
≤x≤2kπ+ ![]() ,k∈Z,
,k∈Z,
∴f(x)的单调递增区间为[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z.
],k∈Z.
(2)解:列表如下:
x | 0 |
|
|
|
| 2π |
x+ |
|
| π |
| 2π |
|
y | 1 | 2 | 0 | ﹣2 | 0 | 1 |
画出函数f(x)在区间[0,2π]上的图象.
【解析】1、根据题意由数量积的坐标运算公式整理,再根据两角和差的正弦公式原式即可整理得到f(x)=2 s i n ( x + ![]() ) ,利用正弦函数的单调增区间由整体思想解得结果。
) ,利用正弦函数的单调增区间由整体思想解得结果。
2、把x+![]() 看作一个整体分别取特殊值
看作一个整体分别取特殊值![]() 、
、![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 即得x的值由描点法可得图像。
即得x的值由描点法可得图像。

练习册系列答案
相关题目