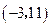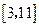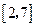题目内容
函数f（x）=2x3+ax2+36x-24在x=2处有极值，则该函数的增区间是（ ）
| A．（-∞，2）∪（3，+∞） | B．（2，3） | C．（-∞，-2）∪（1，+∞） | D．（-2，1） |
y′=f′（x）=6x2+2ax+36，
∵在x=2处有极值，
∴f′（2）=60+4a=0，解得a=-15，
令f′（x）=6x2-30x+36＞0，
解得x＜2或x＞3，
∴该函数的增区间是（-∞，2）∪（3，+∞）．
故选A．
∵在x=2处有极值，
∴f′（2）=60+4a=0，解得a=-15，
令f′（x）=6x2-30x+36＞0，
解得x＜2或x＞3，
∴该函数的增区间是（-∞，2）∪（3，+∞）．
故选A．
练习册系列答案
相关题目
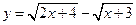的值域 
（
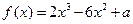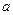是常数）在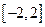
上有最大值3，那么它在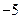
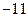
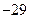
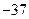
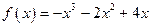，当
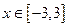时，有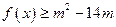
恒成立，则实数
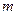的取值范围是
