题目内容
【题目】设函数![]() 的定义城为D,若满足条件:存在
的定义城为D,若满足条件:存在![]() ,使
,使![]() 在
在![]() 上的值城为
上的值城为![]() (
(![]() 且
且![]() ),则称
),则称![]() 为“k倍函数”,给出下列结论:①
为“k倍函数”,给出下列结论:①![]() 是“1倍函数”;②
是“1倍函数”;②![]() 是“2倍函数”:③
是“2倍函数”:③![]() 是“3倍函数”.其中正确的是( )
是“3倍函数”.其中正确的是( )
A.①②B.①③C.②③D.①②③
【答案】D
【解析】
①根据![]() 在
在![]() ,
,![]() 单调递减,可在区间
单调递减,可在区间![]() 上找,也可在区间
上找,也可在区间![]() 上找使
上找使 成立的
成立的![]() 的值.
的值.
②因为![]() ,所以
,所以![]() ,又
,又![]() 在
在![]() 上单调递增,即在区间
上单调递增,即在区间![]() 上找使
上找使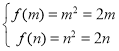 成立的
成立的![]() 的值.
的值.
③![]() 在
在![]() 上单调递增,即找使
上单调递增,即找使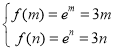 成立的
成立的![]() 的值.等价于
的值.等价于![]() 有两根,可证明
有两根,可证明![]() 有两个零点.
有两个零点.
①![]() 是“1倍函数”:即存在
是“1倍函数”:即存在![]() ,使
,使![]() 在
在![]() 上的值城为
上的值城为![]() .
.
若![]() ,
,![]() 在
在![]() 上单调递减,即
上单调递减,即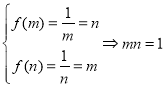 .
.
令![]() ,
,![]() 在
在![]() 上的值域为
上的值域为![]() .
.
即![]() 是“1倍函数”;
是“1倍函数”;
②![]() 是“2倍函数”: 即存在
是“2倍函数”: 即存在![]() ,使
,使![]() 在
在![]() 上的值城为
上的值城为![]() .
.
因为![]() ,所以
,所以![]() .
.
又因为![]() 在
在![]() 上单调递增,即
上单调递增,即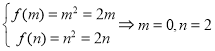 .
.
即![]() 在
在![]() 上的值域为
上的值域为![]() ,即
,即![]() 是“2倍函数”.
是“2倍函数”.
③![]() 是“3倍函数”: 即存在
是“3倍函数”: 即存在![]() ,使
,使![]() 在
在![]() 上的值城为
上的值城为![]() .
.
因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以 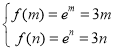 等价于
等价于![]() 有两根.
有两根.
记![]() ,现证
,现证![]() 有两个零点.
有两个零点.
![]() ,令
,令![]() 解得
解得![]() .
.
即函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增.
上单调递增.
![]() ,即
,即![]() 有两个零点.
有两个零点.
即![]() 有两根.
有两根.
即存在![]() ,使
,使![]() 在
在![]() 上的值城为
上的值城为![]() .
.
即![]() 是“3倍函数”.
是“3倍函数”.
综上所述:①②③均正确.
故选:D.

 阅读快车系列答案
阅读快车系列答案【题目】微信作为一款社交软件已经在支付、理财、交通、运动等各方面给人们的生活带来各种各样的便利.手机微信中的“微信运动”,不仅可以看自己每天的运动步数,还可以看到朋友圈里好友的步数.![]() 先生朋友圈里有大量好友使用了“微信运动”这项功能,他随机选取了其中40名,记录了他们某一天的走路步数,统计数据如下表所示:
先生朋友圈里有大量好友使用了“微信运动”这项功能,他随机选取了其中40名,记录了他们某一天的走路步数,统计数据如下表所示:
步数 性别 |
|
|
|
|
|
|
男 | 3 | 4 | 5 | 4 | 3 | 1 |
女 | 3 | 5 | 3 | 2 | 5 | 2 |
(1)以样本估计总体,视样本频率为概率,在![]() 先生的微信朋友圈里的男性好友中任意选取3名,其中走路步数不低于6000步的有
先生的微信朋友圈里的男性好友中任意选取3名,其中走路步数不低于6000步的有![]() 名,求
名,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)如果某人一天的走路步数不低于8000步,此人将被“微信运动”评定为“运动达人”,否则为“运动懒人”.根据题意完成下面的2×2列联表,并据此判断能否有90%以上的把握认为“评定类型”与“性别”有关?
运动达人 | 运动懒人 | 总计 | |
男 | |||
女 | |||
总计 |
附: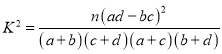 ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |