题目内容
【题目】已知四边形![]() 为等腰梯形,
为等腰梯形, ![]() ,
, ![]() 沿对角线将
沿对角线将![]() 旋转,使得点
旋转,使得点![]() 至点
至点![]() 的位置,此时满足
的位置,此时满足![]() .
.
(1)判断![]() 的形状,并证明;
的形状,并证明;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
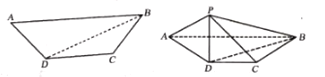
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)由题意可得: ![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,进而得到
,进而得到![]() ,
,
又![]() ,故
,故![]() 为直角三角形;
为直角三角形;
(2)建立空间直角坐标系,求出两个半平面的法向量,代入公式即可得到二面角![]() 的平面角的余弦值,进而得正弦值.
的平面角的余弦值,进而得正弦值.
试题解析:
(1)![]() 为等腰直角三角形,
为等腰直角三角形,
证明:在等腰梯形![]() 中,由平面几何知识可得
中,由平面几何知识可得![]() ,又
,又![]() ,
,
由余弦定理得![]() ,则
,则![]() ,故
,故![]() ,
,
折叠后![]() ,又
,又![]() ,故
,故![]() 平面
平面![]() ,
,
而![]() 面
面![]() ,故
,故![]() ,
,
又![]() ,故
,故![]() 为直角三角形.
为直角三角形.
(2)由(1)知![]() 平面
平面![]() ,
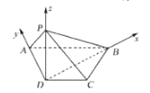
, ![]() ,以点
,以点![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线分别为
所在的直线分别为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则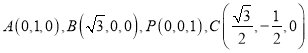 ,
,
则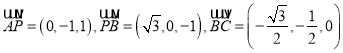 ,
,
平面![]() 的法向量为
的法向量为![]() ,则
,则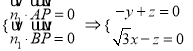 ,
,
取![]() 故,
故, ![]() ,
,
同理可求得平面![]() 的一个法向量
的一个法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则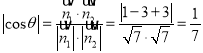 ,
,
结合图形可知![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .美国高中生答题情况是:家占
.美国高中生答题情况是:家占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .为了考察高中生的“恋家(在家里感到最幸福)”是否与国别有关,构建了如下
.为了考察高中生的“恋家(在家里感到最幸福)”是否与国别有关,构建了如下![]() 列联表.
列联表.
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
(Ⅰ)请将![]() 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有![]() 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;
(Ⅱ)从中国高中生的学生中以“是否恋家”为标准采用分层抽样的方法,随机抽取了5人,再从这5人中随机抽取2人.若所选2名学生中的“恋家”人数为![]() ,求随机变量
,求随机变量![]() 的分布列及期望.
的分布列及期望.
附: 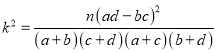 ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |


