题目内容
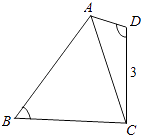
【题目】如图所示，在四边形ABCD中，∠D=2∠B，且AD=1，CD=3，cos∠B= 
（1）求△ACD的面积；
（2）若BC=2 
，求AB的长．
【答案】
（1）解：因为∠D=2∠B，cos∠B= 
，
所以cosD=cos2B=2cos2B﹣1=﹣ 
．
因为∠D∈（0，π），
所以sinD= 
．
因为 AD=1，CD=3，
所以△ACD的面积S= 
= 
= 
．
（2）解：在△ACD中，AC2=AD2+DC2﹣2ADDCcosD=12．
所以AC=2 
．
因为BC=2 ， 
，
所以 
= 
．
所以 AB=4．
【解析】（1）利用已知条件求出D角的正弦函数值，然后求△ACD的面积；（2）利用余弦定理求出AC，通过BC=2 ，利用正弦定理求解AB的长．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
【题目】某公司今年一月份推出新产品A，其成本价为492元/件，经试销调查，销售量与销售价的关系如下表：
销售价（x/元件） | 650 | 662 | 720 | 800 |
销售量（y件） | 350 | 333 | 281 | 200 |
由此可知，销售量y（件）与销售价x（元/件）可近似看作一次函数y=kx+b的关系（通常取表中相距较远的两组数据所得一次函数较为精确）．
（1）写出以x为自变量的函数y的解析式及定义域；
（2）试问：销售价定为多少时，一月份销售利润最大？并求最大销售利润和此时的销售量．
