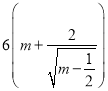题目内容
【题目】设函数![]() ,m∈R.
,m∈R.
(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数![]() 零点的个数.
零点的个数.
【答案】(1)当x=e时,f(x)取得极小值2(2)见解析
【解析】试题分析:(1)求函数的导数![]() ,函数的极值点为
,函数的极值点为![]() ,所以得到函数的单调区间,也就得到函数的最小值了;(2)根据
,所以得到函数的单调区间,也就得到函数的最小值了;(2)根据![]() ,参变分离后得到
,参变分离后得到![]() ,设
,设![]() ,通过导数求函数的单调性,以及图象特征,转化为
,通过导数求函数的单调性,以及图象特征,转化为![]() 与函数的交点个数问题.
与函数的交点个数问题.
试题解析:(1)当![]() 时,
时, ![]() ,∴
,∴![]()
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是增函;
上是增函;
∴当![]() 时,
时, ![]() 取最小值
取最小值![]() .
.
(2)∵函数![]() ,
,
令![]() ,得
,得![]() ;
;
设![]() ,则
,则![]()
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 是
是![]() 的极值点,且是唯一极大值点,∴
的极值点,且是唯一极大值点,∴![]() 是
是![]() 的最大值点;
的最大值点;
∴![]() 的最大值为
的最大值为![]() ,又
,又![]() 结合
结合![]() 的图像,
的图像,
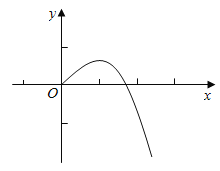
可知:
①当![]() 时,函数
时,函数![]() 无零点;
无零点;
②当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
③当![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
④当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
综上:
当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有且只有一个零点;当
有且只有一个零点;当![]() 时,函数
时,函数![]() 有且只有两个零点.
有且只有两个零点.

练习册系列答案
相关题目