题目内容
((本小题满分12分)
设函数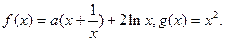
(I)若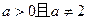 ,直线l与函数
,直线l与函数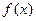 和函数
和函数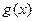 的图象相切于一点,求切线l的方程。
的图象相切于一点,求切线l的方程。
(II)若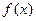 在[2,4]内为单调函数,求实数a的取值范围;
在[2,4]内为单调函数,求实数a的取值范围;
设函数
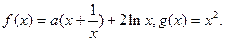
(I)若
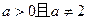 ,直线l与函数
,直线l与函数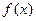 和函数
和函数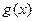 的图象相切于一点,求切线l的方程。
的图象相切于一点,求切线l的方程。(II)若
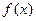 在[2,4]内为单调函数,求实数a的取值范围;
在[2,4]内为单调函数,求实数a的取值范围;解:(Ⅰ)∵
 =
= ,∴
,∴
因为直线
 与函数
与函数 的图象相切于同一点
的图象相切于同一点
 ……………………………………………………………4分
……………………………………………………………4分解得
 (
( ),(
),( 舍去)
舍去) ,
, ;
;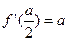 ,
,
 ,
, ;
; ,
,
①当
 时,则
时,则 的方程为:
的方程为:
②当
 时,又因为点(
时,又因为点( 也在
也在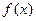
有
 即
即
令
 ,
,
易得方程在

 一定有解
一定有解所以
 的方程为
的方程为
综上所述直线
 的方程为
的方程为 或
或 ………………6分
………………6分(Ⅱ)∵
 =
=
要使
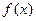 在[2,4]为单调增函数,须
在[2,4]为单调增函数,须 在[2,4]恒成立,
在[2,4]恒成立,即

 在[2,4]恒成立,即
在[2,4]恒成立,即 在[2,4]恒成立,
在[2,4]恒成立,又
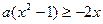 即
即 (
( ) ……………………8分
) ……………………8分设
 (
( ),因为
),因为 (
( )所以
)所以 在
在 )上单调递减.
)上单调递减.
所以当
 时,
时,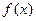 在[2,4]为单调增函数;………………………………10分
在[2,4]为单调增函数;………………………………10分同理要使
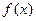 为单调减函数,须
为单调减函数,须 在[2,4]恒成立,
在[2,4]恒成立,易得

综上,若
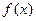 在[2,4]为单调函数,则
在[2,4]为单调函数,则 的取值范围为
的取值范围为 或
或 …12分
…12分略

练习册系列答案
相关题目

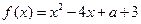 ,
,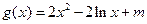
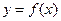 在[-1,1]上存在零点,求实数
在[-1,1]上存在零点,求实数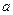 的取值范围;
的取值范围;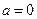 时,若对任意的
时,若对任意的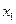 ∈[1,4],总存在
∈[1,4],总存在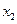 ∈[1,4],使
∈[1,4],使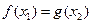 成立,求实数
成立,求实数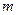 的取值范围;
的取值范围;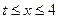 )的值域为区间D,是否存在常数
)的值域为区间D,是否存在常数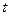 ,使区间D的长度为
,使区间D的长度为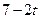 ?若存在,求出
?若存在,求出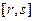 的长度为
的长度为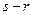 ).
).
 ,则
,则 ( )
( )


 ,
,
 ,n∈N,
,n∈N, ( )
( ) 

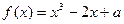 为奇函数,则其图象在点
为奇函数,则其图象在点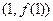 处的切线方程为__________。
处的切线方程为__________。 ,若
,若 在R上可导,则
在R上可导,则 = 。
= 。