题目内容
已知数列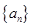 满足
满足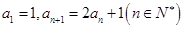
(Ⅰ)求数列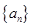 的通项公式;
的通项公式;
(Ⅱ)若数列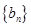 满足
满足 ,证明:
,证明: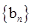 是等差数列;
是等差数列;
(Ⅲ)证明: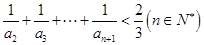
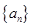 满足
满足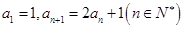
(Ⅰ)求数列
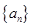 的通项公式;
的通项公式;(Ⅱ)若数列
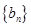 满足
满足 ,证明:
,证明: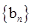 是等差数列;
是等差数列;(Ⅲ)证明:
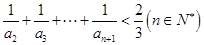
(1)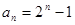 ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
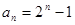 ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.(1)利用递推关系式找出相邻项的关系,从而利用数列的概念求出数列通项公式;(2)先化简所给式子,然后利用式子构造递推式子,作差化简得到等差数列中项的式子即可证明;(3)利用放缩法证明不等式,证明时要注意适当放缩。
解:(1)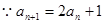 ,
,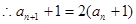
故数列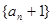 是首项为2,公比为2的等比数列。
是首项为2,公比为2的等比数列。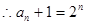 ,
,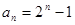
(2)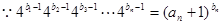 ,
,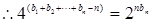
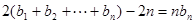 ①
①
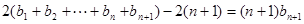 ②
②
②—①得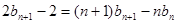 ,即
,即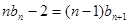 ③
③
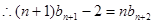 ④ ④—③得
④ ④—③得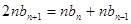 ,即
,即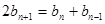
所以数列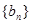 是等差数列
是等差数列
(3)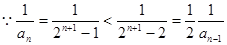
设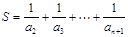 ,
,
则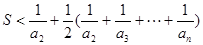
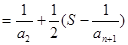
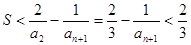
解:(1)
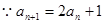 ,
,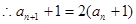
故数列
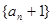 是首项为2,公比为2的等比数列。
是首项为2,公比为2的等比数列。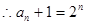 ,
,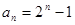
(2)
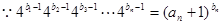 ,
,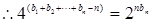
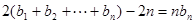 ①
①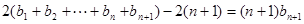 ②
②②—①得
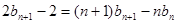 ,即
,即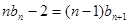 ③
③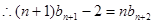 ④ ④—③得
④ ④—③得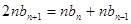 ,即
,即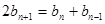
所以数列
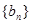 是等差数列
是等差数列(3)
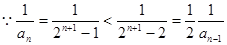
设
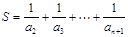 ,
,则
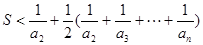
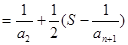
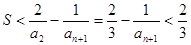

练习册系列答案
相关题目
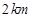 ,以后每秒通过的路程都增加
,以后每秒通过的路程都增加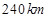 的高度时,火箭与飞船分离,这一过程需要的时间大约是 秒钟;
的高度时,火箭与飞船分离,这一过程需要的时间大约是 秒钟;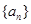 的前n项和为
的前n项和为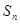 ,且
,且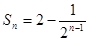 ,数列
,数列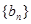 为等差数列,且
为等差数列,且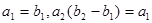 .
. ,求数列
,求数列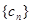 的前n项和
的前n项和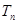 .
.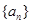 为等差数列,
为等差数列, 为正项等比数列,公比q≠1,若
为正项等比数列,公比q≠1,若 ,则( )
,则( ) ,
,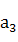 ,
,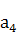 成等比数列,则
成等比数列,则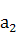 等于( )
等于( )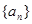 为等差数列,若
为等差数列,若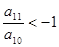 ,且它们的前
,且它们的前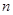 项和
项和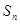 有最大值,则使
有最大值,则使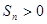 的
的
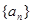 中,已知
中,已知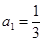 ,
,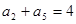 ,
,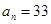 ,则
,则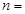 ( )
( )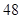
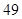
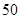

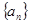 中,
中,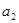 =3,
=3,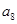 =9,则前9项和
=9,则前9项和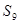 =( )
=( )