题目内容
(14分)已知f(x)是定义在[—1,1]上的奇函数,且f (1)=1,若m,n∈[—
1,1],m+n≠0时有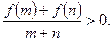
(1)判断f (x)在[—1,1]上的单调性,并证明你的结论;
(2)解不等式: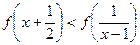 ;
;
(3)若f (x)≤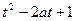 对所有x∈[—1,1],
对所有x∈[—1,1],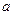 ∈[—1,1]恒成立,求实数t的取值范围.
∈[—1,1]恒成立,求实数t的取值范围.
1,1],m+n≠0时有
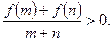
(1)判断f (x)在[—1,1]上的单调性,并证明你的结论;
(2)解不等式:
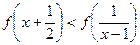 ;
;(3)若f (x)≤
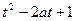 对所有x∈[—1,1],
对所有x∈[—1,1],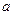 ∈[—1,1]恒成立,求实数t的取值范围.
∈[—1,1]恒成立,求实数t的取值范围.解:(1)任取—1≤x1<x2≤1,则
f (x1)—f (x2)=" f" (x1)+f (-x2)=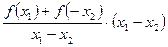
∵—1≤x1<x2≤1,∴x1+(-x2)≠0,
由已知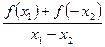 >0,又x1-x2<0,
>0,又x1-x2<0,
∴f (x1)—f (x2)<0,即f (x)在[—1,1]上为增函数.
(2) ∵f (x)在[—1,1]上为增函数,故有
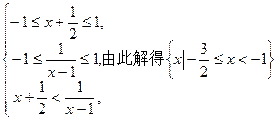
(3)由(1)可知:f(x)在[—1,1]上是增函数,且f (1)=1,故对x∈[—l,1],恒有f(x)≤1.
所以要使f(x)≤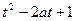 ,对所有x∈[—1,1],
,对所有x∈[—1,1],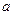 ∈[—1,1]恒成立,
∈[—1,1]恒成立,
即要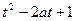 ≥1成立,故
≥1成立,故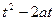 ≥0成立.
≥0成立.
记g(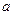 )=
)=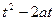 对
对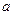 ∈[—1,1],g(
∈[—1,1],g(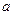 )≥0恒成立,只需g(
)≥0恒成立,只需g(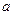 )在[—1,1]上的最小值大于等于零.
)在[—1,1]上的最小值大于等于零.
故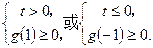
解得:t≤—2或t=0.
f (x1)—f (x2)=" f" (x1)+f (-x2)=
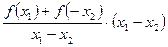
∵—1≤x1<x2≤1,∴x1+(-x2)≠0,
由已知
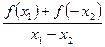 >0,又x1-x2<0,
>0,又x1-x2<0,∴f (x1)—f (x2)<0,即f (x)在[—1,1]上为增函数.
(2) ∵f (x)在[—1,1]上为增函数,故有
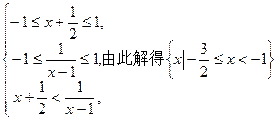
(3)由(1)可知:f(x)在[—1,1]上是增函数,且f (1)=1,故对x∈[—l,1],恒有f(x)≤1.
所以要使f(x)≤
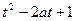 ,对所有x∈[—1,1],
,对所有x∈[—1,1],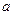 ∈[—1,1]恒成立,
∈[—1,1]恒成立,即要
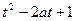 ≥1成立,故
≥1成立,故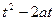 ≥0成立.
≥0成立.记g(
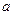 )=
)=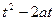 对
对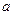 ∈[—1,1],g(
∈[—1,1],g(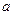 )≥0恒成立,只需g(
)≥0恒成立,只需g(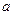 )在[—1,1]上的最小值大于等于零.
)在[—1,1]上的最小值大于等于零.故
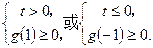
解得:t≤—2或t=0.
略

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
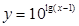 的图象相同的函数是 ( )
的图象相同的函数是 ( )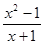
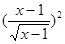
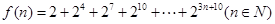 ,则
,则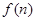 等于( )
等于( )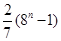
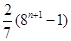
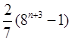
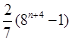
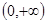 上单调递增的是
上单调递增的是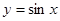
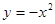
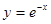
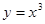
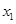 ,
,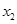 (
(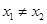 ).
). 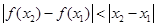 恒成立”的只有( )
恒成立”的只有( ) 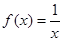
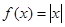
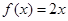
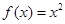
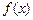 在
在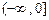 内单调递减,则不等式
内单调递减,则不等式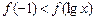 的解集是 .
的解集是 .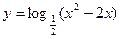 的单调递增区间是_________________.
的单调递增区间是_________________.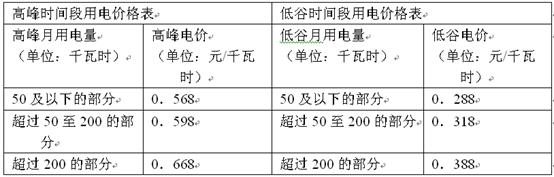
 家庭5月份的高峰时间段用电量为
家庭5月份的高峰时间段用电量为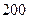 千瓦时,低谷时间段用电量为
千瓦时,低谷时间段用电量为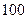 千瓦时,
千瓦时, 费为 元(用数字作答)
费为 元(用数字作答)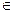 [0,1],则函数y=
[0,1],则函数y=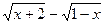 的值域是
的值域是