题目内容
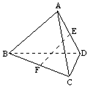在三棱锥A-BCD中，平面ABD⊥平面BCD，∠BDC=90°，E、F分别是AD、BC的中点，若EF=CD，则EF与平面ABD所成的角为30°
30°
．分析：要求线面角，关键是寻找平面的垂线． 利用面面垂直，易得平面的垂线，从而得解．
解答：解：取BD的中点O，连接OE，OF
∵F是BC的中点，∴OF∥CD
∵∠BDC=90°，∴OF⊥BD
∵平面ABD⊥平面BCD
∴∠OEF 为EF与平面ABD所成的角
∵EF=CD
∴OF=
EF
∴∠OEF=30°
∴EF与平面ABD所成的角为30°
故答案为30°
∵F是BC的中点，∴OF∥CD
∵∠BDC=90°，∴OF⊥BD
∵平面ABD⊥平面BCD
∴∠OEF 为EF与平面ABD所成的角
∵EF=CD
∴OF=
| 1 |
| 2 |
∴∠OEF=30°
∴EF与平面ABD所成的角为30°
故答案为30°
点评：本题的考点是直线与平面所成的角，主要考查线面角，关键是寻找平面的垂线．
练习册系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
如图，在三棱锥A-BCD中，DA，DB，DC两两垂直，且长度均为1，E为BC中点，则下列结论正确的是（ ）
在三棱锥A-BCD中，AB=4，CD=2，且异面直线AB、CD所成的角为60°，若M、N分别是AD、BC的中点，则MN=
（2011•渭南三模）在三棱锥A-BCD中，BD=BC=1，BD⊥BC，DE⊥AB，AD=2，AD⊥平面BCD．
如图所示，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜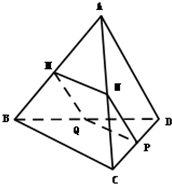
如图，在三棱锥A-BCD中，平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点，且MN=PQ．