题目内容
7．由直线x=0，x=2，y=0与曲线y=ex所围成的封闭图形的面积为（ ）| A． | e2 | B． | e | C． | e2-1 | D． | e2+1 |
分析 利用定积分的几何意义得出直线x=0，x=2，y=0与曲线y=ex所围成的封闭图形的面积为S，计算即可．
解答 解：设直线x=0，x=2，y=0与曲线y=ex所围成的封闭图形的面积为S，
根据积分的几何意义得出：S=${∫}_{0}^{2}$exdx=ex|${\;}_{0}^{2}$=e2-e0=e2-1
故选：C．
点评 本题主要考查了定积分在求面积中的应用，以及定积分的计算，属于基础题
练习册系列答案
百分学生作业本题练王系列答案
互动课堂系列答案
相关题目
18．正项等比数列{an}中的a1，a9是函数f（x）=$\frac{1}{3}{x^3}-a{x^2}$+x+1的极值点，则lna5=（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 与a的值有关 |
15．设△ABC的内角A、B、C所对的边分别为a，b，c，若bcosC+ccosB=asinA，则△ABC的形状为（ ）
| A． | 锐角三角形 | B． | 钝角三角形 | C． | 直角三角形 | D． | 等腰直角三角形 |
2．复平面上表示复数z=1-i（i为虚数单位）的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
19．抛物线x2=2y的焦点到准线的距离是（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{4}$ | D． | $\frac{1}{8}$ |
16．如图，在矩形ABCD中，AB=$\sqrt{3}$，BC=1，E为线段CD上一动点，现将△AED沿AE折起，使平面AED⊥平面ABC，当E从D运动到C，则D在平面ABC上的射影K所形成轨迹的长度为（ ）
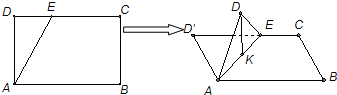
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{3}$ |
函数f（x）的定义域为R，f（-1）=2，f′（x）为f（x）的导函数，已知y=f′（x）的图象如图所示，则f（x）＞2x+4的解集为（-1，+∞）．