题目内容
12.$\int\begin{array}{l}1\\-1\end{array}\sqrt{1-{x^2}}\;dx$=$\frac{π}{2}$.分析 根据定积分的几何意义求值.
解答 解:已知$\int\begin{array}{l}1\\-1\end{array}\sqrt{1-{x^2}}\;dx$表示以原点为圆心,半径为1的半圆的面积;故$\int\begin{array}{l}1\\-1\end{array}\sqrt{1-{x^2}}\;dx$=$\frac{π}{2}$;
故答案为:$\frac{π}{2}$.
点评 本题考查了利用定积分的几何意义求定积分的值.属于基础题.

练习册系列答案
相关题目
20.已知f(x)=log2(x2-ax+3a)在[2,+∞)上是增函数,则实数a的取值范围是( )
| A. | (-∞,4) | B. | (-4,4] | C. | (-∞,-4)∪[2,+∞) | D. | [-4,4) |
7.由直线x=0,x=2,y=0与曲线y=ex所围成的封闭图形的面积为( )
| A. | e2 | B. | e | C. | e2-1 | D. | e2+1 |
17.复数$z=3i+\frac{2}{1+i}$(i是虚数单位)在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
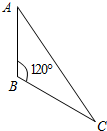 在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,
在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,