题目内容
【题目】在直角坐标系中,曲线C的参数方程: ![]() ,直线l的参数方程为
,直线l的参数方程为 ![]() .
.
(1)若直线l与曲线C只有一个公共点,求实数a;
(2)若点P,Q分别为直线l与曲线C上的动点,若 ![]() ,求实数a.
,求实数a.
【答案】
(1)解:∵曲线C的参数方程: 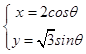 ,
,
∴曲线C的普通方程为 ![]() =1,
=1,
∵直线l的参数方程为 ![]() ,
,
∴直线l的普通方程为x+2y﹣a﹣2=0,
联立 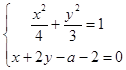 ,得16y2﹣(12a+24)y+3a2+12a=0,
,得16y2﹣(12a+24)y+3a2+12a=0,
∵直线l与曲线C只有一个公共点,
∴△=[﹣(12a+24)]2﹣4×16×(3a2+12a)=﹣a2﹣4a+12=0,
解得a=2或a=﹣6
(2)解:设Q(2cosθ, ![]() ),
),
点Q到直线l的距离d= 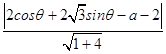 =
= ![]() |4sin(
|4sin( ![]() )﹣a﹣2|,
)﹣a﹣2|,
∵点P,Q分别为直线l与曲线C上的动点, ![]() ,
,
∴当sin( ![]() )=1时,|PQ|min=
)=1时,|PQ|min= ![]() |2﹣a|=
|2﹣a|= ![]() ,
,
解得a=1或a=3
【解析】(1)由曲线C的参数方程求出曲线C的普通方程为 ![]() =1,由直线l的参数方程求出直线l的普通方程为x+2y﹣a﹣2=0,联立
=1,由直线l的参数方程求出直线l的普通方程为x+2y﹣a﹣2=0,联立 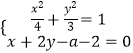 ,得16y2﹣(12a+24)y+3a2+12a=0,由直线l与曲线C只有一个公共点,利用根的判别式为0,能求出a.(2)设Q(2cosθ,
,得16y2﹣(12a+24)y+3a2+12a=0,由直线l与曲线C只有一个公共点,利用根的判别式为0,能求出a.(2)设Q(2cosθ, ![]() ),求出点Q到直线l的距离d=
),求出点Q到直线l的距离d= ![]() |4sin(
|4sin( ![]() )﹣a﹣2|,由题意知当sin(
)﹣a﹣2|,由题意知当sin( ![]() )=1时,|PQ|min=
)=1时,|PQ|min= ![]() |2﹣a|=
|2﹣a|= ![]() ,由此能求出a.
,由此能求出a.

练习册系列答案
相关题目

