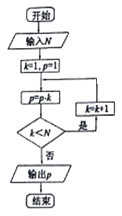
题目内容
【题目】已知长方体ABCD﹣A1B1C1D1内接于球O,底面ABCD是正方形,E为AA1的中点,OA⊥平面BDE,则 ![]() = .
= .
【答案】![]()
【解析】解:以D为原点,建立空间直角坐标系O﹣xyz,
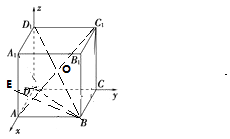
设AB=a,AA1=c,
则A(a,0,0),E(a,0, ![]() ),D(0,0,0),
),D(0,0,0),
B(a,a,0),D(0,0,c),O( ![]() ),
),
![]() =(a,0,
=(a,0, ![]() ),
), ![]() =(a,a,0),
=(a,a,0),
![]() =(
=( ![]() ),
),
∵OA⊥平面BDE,
∴ 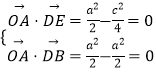 ,解得c=
,解得c= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用棱柱的结构特征的相关知识可以得到问题的答案,需要掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.

练习册系列答案
相关题目