题目内容
已知函数f(x)=cos(
x+
)
(1)用“五点法”作图作出y=f(x)的一个周期的图象;(列表作图)
(2)求函数f(x)的最大值,并写出取得最大值时自变量x的取值集合;
(3)函数y=f(x)可以由函数y=cosx如何变化得到?写出变化过程.
| π |
| 6 |
| π |
| 2 |
(1)用“五点法”作图作出y=f(x)的一个周期的图象;(列表作图)
(2)求函数f(x)的最大值,并写出取得最大值时自变量x的取值集合;
(3)函数y=f(x)可以由函数y=cosx如何变化得到?写出变化过程.
考点:五点法作函数y=Asin(ωx+φ)的图象,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)根据题意,列出表格,并画出函数f(x)在一个周期[-3,9]上的图象;
(2)求出函数f(x)的最大值以及对应的自变量x的取值集合;
(3)方法一,先把横坐标变为原来的
倍,再向左平移3个单位;
方法二,先向左平移
个单位,再把横坐标变化成原来的
倍.
(2)求出函数f(x)的最大值以及对应的自变量x的取值集合;
(3)方法一,先把横坐标变为原来的
| 6 |
| π |
方法二,先向左平移
| π |
| 2 |
| 6 |
| π |
解答:
解:(1)根据题意,列表如下:
画出函数f(x)=cos(
x+
)在周期[-3,9]上的图象,如图所示
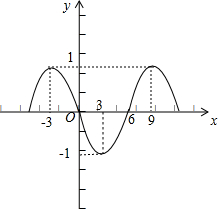
(2)函数f(x)=cos(
x+
)的最大值是f(x)max=1,
令
x+
=2kπ,k∈Z,
解得x=-3+12k,k∈Z,
即函数取得最大值时自变量x的取值集合是{x|x=-3+12k,k∈Z};
(3)方法一,由函数y=cosx图象的横坐标变换成原来的
倍,再向左平移3个单位,即得函数y=f(x)的图象;
方法二,由函数y=cosx向左平移
个单位,再把横坐标变化成原来的
倍,即得函数y=f(x)的图象.
| 0 |
| π |
| 2π | ||||||||
| x | -3 | 0 | 3 | 6 | 9 | ||||||||
f(x)=cos(
| 1 | 0 | -1 | 0 | 1 |
| π |
| 6 |
| π |
| 2 |

(2)函数f(x)=cos(
| π |
| 6 |
| π |
| 2 |
令
| π |
| 6 |
| π |
| 2 |
解得x=-3+12k,k∈Z,
即函数取得最大值时自变量x的取值集合是{x|x=-3+12k,k∈Z};
(3)方法一,由函数y=cosx图象的横坐标变换成原来的
| 6 |
| π |
方法二,由函数y=cosx向左平移
| π |
| 2 |
| 6 |
| π |
点评:本题考查了余弦函数的图象与性质的应用问题,解题时应对函数解析式进行分析,利用整体思想求解,是基础题目.

练习册系列答案
相关题目
若0<x<
,0<y<
,且sinx=xcosy,则( )
| π |
| 2 |
| π |
| 2 |
A、y<
| ||||
B、
| ||||
C、
| ||||
| D、x<y |
表面积为4
的正四面体的各个顶点都在同一个球面上,则此球的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各组函数f(x)与g(x)的图象相同的是( )
A、f(x)=x,g(x)=(
| |||||
| B、f(x)=x2,g(x)=(x+1)2 | |||||
C、f(x)=|x|,g(c)=
| |||||
| D、f(x)=1,g(x)=x0 |