题目内容
【题目】数列{an}满足a1=1,a2=2,an+2=![]() ,n=1,2,3,….求a3,a4,并求数列{an}的通项公式;
,n=1,2,3,….求a3,a4,并求数列{an}的通项公式;
【答案】见解析
【解析】试题分析:根据an+2=![]() ,把a1和a2代入即可求得a3, a4,先看当n=2k-1时,整理得
,把a1和a2代入即可求得a3, a4,先看当n=2k-1时,整理得![]() -
-![]() =1进而可判断数列{
=1进而可判断数列{![]() }是首项为1、公差为1的等差数列; n=2k时,整理得
}是首项为1、公差为1的等差数列; n=2k时,整理得![]() =2
=2![]() 进而可判断数列{
进而可判断数列{![]() }是首项为2、公比为2的等比数列,最后综合可得答案.
}是首项为2、公比为2的等比数列,最后综合可得答案.
试题解析:∵a1=1,a2=2,
∴a3=![]() =a1+1=2,
=a1+1=2,
a4=(![]() π)a2+
π)a2+![]() π=2a2=4,
π=2a2=4,
当n=2k-1时,a2k+1=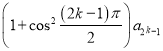 +
+
![]() =
=![]() +1,即
+1,即![]() -
-![]() =1,
=1,
所以数列{![]() }是首项为1,公差为1的等差数列,因此
}是首项为1,公差为1的等差数列,因此![]() =1+(k-1)=k,
=1+(k-1)=k,
当n=2k时, ![]() =
=![]() +
+![]() =2
=2![]() ,
,
所以数列{![]() }是首项为2,公比为2的等比数列,因此
}是首项为2,公比为2的等比数列,因此![]() =
=![]() .
.
故数列{an}的通项公式为an=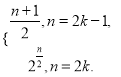

【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: