题目内容
13．已知3A${\;}_{8}^{n}$=4A${\;}_{9}^{n-1}$，求n的值．分析 由已知条件利用排列数公式，得3×8×7×…×（9-n）=4×9×8×7×…×（11-n），由此能求出m．
解答 解：∵3A8n=4A9n-1，
∴3×8×7×…×（9-n）=4×9×8×7×…×（11-n），
∴3（10-n）（11-n）=4×9，
整理，得n2-21n+98=0，
解得n=7或n=14（舍），
∴n=7．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意排列数公式的合理运用．
练习册系列答案
相关题目
4．已知△ABC中，内角A，B，C所对的边长分别为a，b，c．若a=2bcosA，B=$\frac{π}{3}$，c=1，则△ABC的面积等于（ ）
| A． | $\frac{{\sqrt{3}}}{8}$ | B． | $\frac{{\sqrt{3}}}{6}$ | C． | $\frac{{\sqrt{3}}}{4}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
1．在平面直角坐标系中，把横、纵坐标均为有理数的点称为有理点．若a为无理数，则在过点P（a，-$\frac{1}{2}$）的所有直线中（ ）
| A． | 有无穷多条直线，每条直线上至少存在两个有理点 | |
| B． | 恰有n（n≥2）条直线，每条直线上至少存在两个有理点 | |
| C． | 有且仅有一条直线至少过两个有理点 | |
| D． | 每条直线至多过一个有理点 |
5．
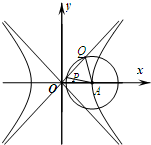如图，已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q．若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$，则双曲线C的离心率为（ ）
如图，已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q．若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$，则双曲线C的离心率为（ ）| A． | $\sqrt{3}$ | B． | $\frac{2\sqrt{13}}{5}$ | C． | $\frac{\sqrt{7}}{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
2．下列四个命题中正确命题的是（ ）
| A． | 学校抽取每个班级座号为21-30号的同学检查作业完成情况，这是分层抽样 | |
| B． | 可以通过频率分布直方图中最高小矩形的高来估计这组数据的众数 | |
| C． | 设随机变量ξ服从正态分布N（0，1），若P（ξ＞1）=p，则P（-1＜ξ＜0）=1-p | |
| D． | 在散点图中，回归直线至少经过一个点 |
3．若集合A={x|2${\;}^{{x}^{2}-4x-5}$＞1}，集合B={x|y=lg$\frac{2-x}{2+x}$}，则A∩B=（ ）
| A． | {x|-5＜x＜1} | B． | {x|-2＜x＜1} | C． | {x|-2＜x＜-1} | D． | {x|-5＜x＜-1} |