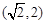题目内容
如图,在△ABC中,∠ABC=90°,AB=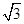 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
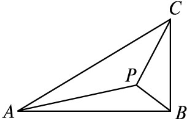
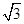 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.(1)若PB=
 ,求PA;
,求PA;(2)若∠APB=150°,求tan∠PBA.

(1)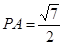 (2)
(2)
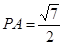 (2)
(2)
试题分析:(1)在三角形中,两边和一角知道,该三角形是确定的,其解是唯一的,利用余弦定理求第三边.(2)利用同角三角函数的基本关系求角的正切值.(3)若是已知两边和一边的对角,该三角形具有不唯一性,通常根据大边对大角进行判断.(4)在三角兴中,注意
 这个隐含条件的使用.
这个隐含条件的使用.试题解析:解:(1)由已知得∠PBC=60°,所以∠PBA=30°.
在△PBA中,由余弦定理得PA2=
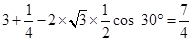 .
.故PA=
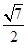 . 5分
. 5分(2)设∠PBA=α,由已知得PB=sin α.
在△PBA中,由正弦定理得
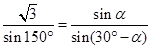 ,
,化简得
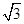 cos α=4sin α.
cos α=4sin α.所以tan α=
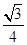 ,即tan∠PBA=
,即tan∠PBA=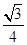 . 12分
. 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
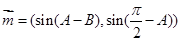 ,
,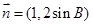 ,
,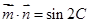 ,其中A,B,C分别为△ABC的三边
,其中A,B,C分别为△ABC的三边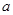 ,
,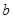 ,
,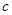 所对的角.
所对的角.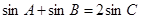 ,且S△ABC=
,且S△ABC=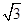 ,求边c的长
,求边c的长 <
< <
< <
<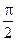 ,
,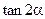 的值.(Ⅱ)求
的值.(Ⅱ)求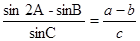 ,则角A的大小为( ).
,则角A的大小为( ).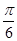
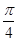
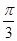
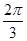
 中,若
中,若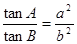 ,则
,则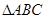 中,角A、B、C的对应边分别为
中,角A、B、C的对应边分别为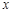 、
、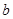 、
、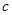 ,若满足
,若满足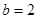 ,
,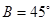 的
的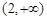 B.
B. C.
C. D.
D.