题目内容
已知A={x||x2-mx+m|≤1},若[-1,1]⊆A,则实数m的取值范围为( )
| A.(-∞,0] | B.[2-2
| C.(-∞,-2] | D.[2-2
|
令f(x)=x2-mx+m,其对称轴x=-
.
①当-
≤-1,即m≥2时,f(x)在[-1,1]上单调递增,∵[-1,1]⊆A,∴
,解得-1≤m≤0,不满足m≥2,应舍去;
②当-
≥1,即m≤-2时,f(x)在[-1,1]上单调递减,∵[-1,1]⊆A,∴
,解得-1≤m≤0,不满足m≤-2,应舍去;
③当-1<-
<1,即-2<m<2时,f(x)在[-1,-
]上单调递减,在[
,1]上单调递增,∵[-1,1]⊆A,∴
,解得2-2
≤m≤0,满足-2<m<2,故2-2
≤m≤0.
综上①②③可知:m的取值范围为[2-2
,0].
故选B.
| m |
| 2 |
①当-
| m |
| 2 |
|
②当-
| m |
| 2 |
|
③当-1<-
| m |
| 2 |
| m |
| 2 |
| -m |
| 2 |
|
| 2 |
| 2 |
综上①②③可知:m的取值范围为[2-2
| 2 |
故选B.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
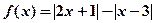 .
.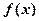 ≤4;
≤4;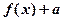 ≤0成立,求实数a的取值范围.
≤0成立,求实数a的取值范围.  (a>0,a≠1).
(a>0,a≠1). 的解集为______________.
的解集为______________.