题目内容
6.已知{an}为等差数列,a3=7,a1+a7=10,前n项和为Sn,则这个数列的公差d=-2,通项公式an=13-2n,使得Sn达到最大值时的n=6.分析 由题意可得首项和公差的方程组,解方程组可得通项,进而可得{an}的前6项为正数,从第7项开始为负数,可得前6项和最大.
解答 解:∵{an}为等差数列,a3=7,a1+a7=10,
∴a3=a1+2d=7,a1+a7=2a1+6d=10,
联立解得a1=11,d=-2,
∴通项公式an=11-2(n-1)=13-2n,
令13-2n≤0可得n≥$\frac{13}{2}$,
∴{an}的前6项为正数,从第7项开始为负数,
∴使得Sn达到最大值时的n=6
故答案为:-2;13-2n;6
点评 本题考查等差数列的求和公式和通项公式,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.若平面α的一个法向量$\overrightarrow n$=(2,1,1),直线l的一个方向向量为$\overrightarrow a$=(1,2,3),则l与α所成角的正弦值为( )
| A. | $\frac{\sqrt{17}}{6}$ | B. | $\frac{\sqrt{21}}{6}$ | C. | -$\frac{\sqrt{21}}{6}$ | D. | $\frac{\sqrt{21}}{3}$ |
17.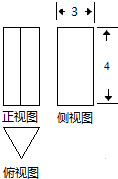 如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
 如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )| A. | 18 | B. | 9$\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
18.设i是虚数单位,则复数$\frac{4+3i}{3-4i}$=( )
| A. | $\frac{4}{5}+\frac{3}{5}i$ | B. | $\frac{4}{25}+\frac{3}{25}i$ | C. | -i | D. | i |