题目内容
2.已知定义域为R的奇函数f(x)满足f(x)=$\left\{\begin{array}{l}\frac{2}{2x-3}(x>2)\\{x^2}-2x+2(0<x≤2)\end{array}$,下列说法:①当-1<x1<x2<1时,f(x1)>f(x2);②直线y=x与函数f(x)的图象有5个交点;③当x∈(0,a]时,f(x)的最小值为1,则a∈[1,$\frac{5}{2}$];④关于x的两个方程f(x)=$\frac{3}{2}$与f(x)=b所有根的和为0,则b=-$\frac{3}{2}$;其中正确的有②③.分析 ①根据函数奇偶性的性质,求出函数f(x)的解析式,判断当-1<x1<x2<1时的函数的单调性.
②作出函数y=x的图象,利用数形结合进行判断.
③求出函数f(x)=1的根,判断a的取值范围即可.
④根据函数奇偶性的对称性进行判断.
解答 解:∵函数f(x)是奇函数,
∴若x<-2,则-x>2,则f(-x)=$\frac{2}{-2x-3}$=-f(x),
则f(x)=$\frac{2}{2x+3}$,x<-2.
若-2≤x<0,则0<-x≤2,则f(-x)=x2+2x+2=-f(x),
即f(x)=-x2-2x-2,-2≤x<0,
当x=0,则f(0)=0.
作出函数f(x)的图象如图:
①当-1<x1<x2<1时,函数f(x)不是单调函数,则f(x1)>f(x2)不成立;
②作出y=x的图象,则直线y=x与函数f(x)的图象有5个交点,成立.
③当x=$\frac{5}{2}$时,f($\frac{5}{2}$)=$\frac{2}{2×\frac{5}{2}-3}$=$\frac{2}{5-3}=\frac{2}{2}=1$,
则当x∈(0,a]时,f(x)的最小值为1,则a∈[1,$\frac{5}{2}$],则成立.
④∵函数f(x)是奇函数,若关于x的两个方程f(x)=$\frac{3}{2}$与f(x)=b所有根的和为0,
∴函数f(x)=$\frac{3}{2}$的根与f(x)=b根关于原点对称,
则b=-$\frac{3}{2}$,
但x>0时,方程f(x)=$\frac{3}{2}$有3个根,
设分别为x1,x2,x3,且0<x1<x2<2<x3,
则有$\frac{2}{2x-3}$=$\frac{3}{2}$得x=$\frac{13}{6}$,即x3=$\frac{13}{6}$,
x1+x22=2,
则三个根之和为2+$\frac{13}{6}$=$\frac{25}{6}$,
若关于x的两个方程f(x)=$\frac{3}{2}$与f(x)=b所有根的和为0,
则f(x)=b的根为-$\frac{25}{6}$,
此时b=f(-$\frac{25}{6}$)=$\frac{2}{2•(-\frac{25}{6})+3}$=-$\frac{6}{16}$=-$\frac{3}{8}$,
故④错误,
故答案为:②③.
点评 本题主要考查命题的真假判断,根据函数的奇偶性的性质,利用数形结合是解决本题的关键.

| A. | 7 | B. | 8 | C. | 9 | D. | 11 |
| A. | (-3,0)∪(3,+∞) | B. | (-3,0)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-∞,-3)∪(0,3) |
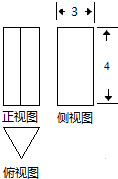 如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )| A. | 18 | B. | 9$\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
| A. | 1 | B. | -1 | C. | i | D. | -i |