题目内容
(本小题满分13分)
已知三棱锥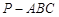 ,
,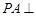 平面
平面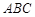 ,
,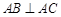 ,
,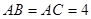 ,
,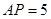 .
.
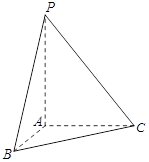
(Ⅰ)把△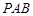 (及其内部)绕
(及其内部)绕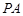 所在直线旋转一周形成一几何体,求该几何体的体积
所在直线旋转一周形成一几何体,求该几何体的体积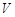 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
已知三棱锥
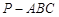 ,
,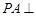 平面
平面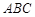 ,
,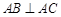 ,
,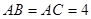 ,
,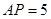 .
.
(Ⅰ)把△
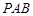 (及其内部)绕
(及其内部)绕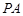 所在直线旋转一周形成一几何体,求该几何体的体积
所在直线旋转一周形成一几何体,求该几何体的体积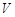 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.(Ⅰ) . (Ⅱ)
. (Ⅱ) .
.
 . (Ⅱ)
. (Ⅱ) .
. 本试题主要是考查了几何体体积的求解,以及二面角的求解的综合运用。
(1)由于由题设,所得几何体为圆锥,其底面半径为4,高为5,根据圆锥的体积公式可知结论。
(2)合理的建立空间直角坐标系,然后表示出点的坐标,和向量的坐标和求解平面的法向量,利用向量的数量积性质,得到向量的夹角,从而得到二面角的平面角的大小。
解:(Ⅰ)由题设,所得几何体为圆锥,其底面半径为 ,高为
,高为 .
.
该圆锥的体积 . ………………5分
. ………………5分
(Ⅱ)如图建立空间直角坐标系,可得各点的坐标 ,
, ,
, ,
, .于是
.于是 ,
, .………………7分
.………………7分
由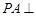 平面
平面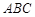 ,得平面
,得平面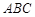 的一个法向量
的一个法向量 .……8分
.……8分
设 是平面
是平面 的一个法向量.
的一个法向量.
因为 ,
, ,所以
,所以 ,
, ,
,
即 ,
, ,解得
,解得 ,
, ,取
,取 ,得
,得 .…10分
.…10分
设 与
与 的夹角为
的夹角为 ,则
,则 . ………12分
. ………12分
结合图可判别二面角 是个锐角,它的余弦值为
是个锐角,它的余弦值为 . ………………13分
. ………………13分
(1)由于由题设,所得几何体为圆锥,其底面半径为4,高为5,根据圆锥的体积公式可知结论。
(2)合理的建立空间直角坐标系,然后表示出点的坐标,和向量的坐标和求解平面的法向量,利用向量的数量积性质,得到向量的夹角,从而得到二面角的平面角的大小。
解:(Ⅰ)由题设,所得几何体为圆锥,其底面半径为
 ,高为
,高为 .
. 该圆锥的体积
 . ………………5分
. ………………5分(Ⅱ)如图建立空间直角坐标系,可得各点的坐标
 ,
, ,
, ,
, .于是
.于是 ,
, .………………7分
.………………7分由
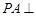 平面
平面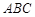 ,得平面
,得平面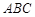 的一个法向量
的一个法向量 .……8分
.……8分设
 是平面
是平面 的一个法向量.
的一个法向量.因为
 ,
, ,所以
,所以 ,
, ,
,即
 ,
, ,解得
,解得 ,
, ,取
,取 ,得
,得 .…10分
.…10分设
 与
与 的夹角为
的夹角为 ,则
,则 . ………12分
. ………12分结合图可判别二面角
 是个锐角,它的余弦值为
是个锐角,它的余弦值为 . ………………13分
. ………………13分
练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
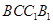 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线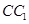 的中点,已知
的中点,已知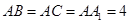
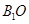 ⊥平面
⊥平面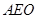 ;
;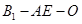 的余弦值.
的余弦值.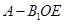 的体积.
的体积. 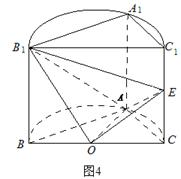
 中,
中, ,
, ,
, 平面
平面 ,
, 为
为  的中点,
的中点, .
.
 ;
; 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面 ;
; 的大小.
的大小. 在圆柱
在圆柱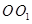 的底面圆
的底面圆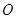 上,
上,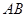 为圆
为圆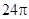 ,
,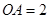 ,
,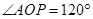 。
。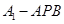 的体积。
的体积。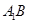 与
与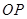 所成角的余弦值;
所成角的余弦值;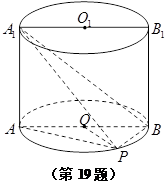
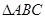 沿
沿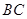 边上的高
边上的高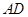 折成直二面角
折成直二面角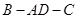 ,则三棱锥
,则三棱锥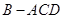 的外接球的表面积为 _________
的外接球的表面积为 _________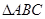 是边长为2的正三角形,俯视图为正六边形,那么该几何体的体积为( )
是边长为2的正三角形,俯视图为正六边形,那么该几何体的体积为( )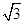
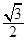
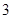
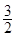
 中,
中, 为正方形且边长为
为正方形且边长为 ,面
,面 面
面 ,
,  ,
, ,
, ,则该组合体的体积为( )
,则该组合体的体积为( )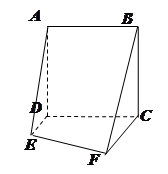



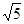 ,BC=AD=
,BC=AD=
 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱 底面
底面 ,且
,且 ,则该四棱锥的体积是( )
,则该四棱锥的体积是( )