题目内容
已知四边形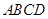 满足
满足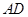 ∥
∥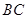 ,
,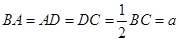 ,
,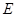 是
是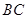 的中点,将
的中点,将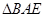 沿着
沿着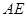 翻折成
翻折成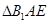 ,使面
,使面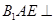 面
面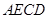 ,
,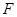 为
为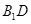 的中点.
的中点.
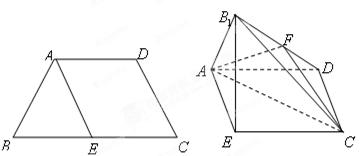
(Ⅰ)求四棱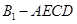 的体积;
的体积;
(Ⅱ)证明: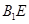 ∥面
∥面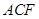 ;
;
(Ⅲ)求面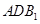 与面
与面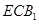 所成二面角的余弦值.
所成二面角的余弦值.
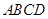 满足
满足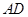 ∥
∥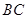 ,
,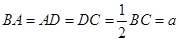 ,
,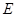 是
是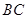 的中点,将
的中点,将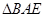 沿着
沿着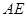 翻折成
翻折成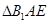 ,使面
,使面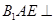 面
面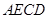 ,
,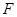 为
为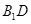 的中点.
的中点. 
(Ⅰ)求四棱
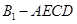 的体积;
的体积;(Ⅱ)证明:
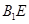 ∥面
∥面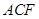 ;
;(Ⅲ)求面
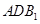 与面
与面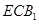 所成二面角的余弦值.
所成二面角的余弦值.(Ⅰ)取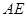 的中点
的中点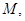 连接
连接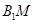 ,因为
,因为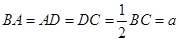 ,
,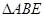 为等边三角形,则
为等边三角形,则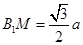 ,又因为面
,又因为面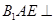 面
面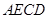 ,所以
,所以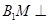 面
面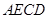 ,
,
所以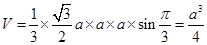 …………4分
…………4分
(Ⅱ)连接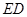 交
交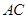 于
于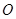 ,连接
,连接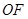 ,因为
,因为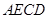 为菱形,
为菱形, ,又
,又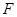 为
为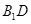 的中点,所以
的中点,所以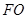 ∥
∥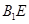 ,所以
,所以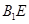 ∥面
∥面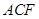 ……………7分
……………7分
(Ⅲ)连接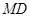 ,分别以
,分别以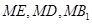 为
为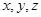 轴
轴
则
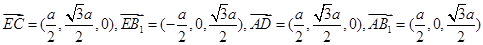 ……9分
……9分
设面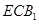 的法向量
的法向量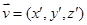 ,
,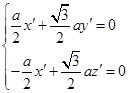 ,令
,令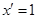 ,则
,则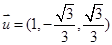
设面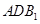 的法向量为
的法向量为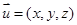 ,
,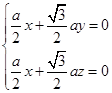 ,令
,令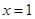 ,则
,则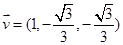 ……11分
……11分
则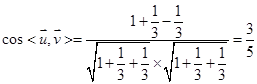 ,所以二面角的余弦值为
,所以二面角的余弦值为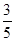
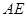 的中点
的中点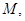 连接
连接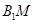 ,因为
,因为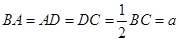 ,
,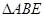 为等边三角形,则
为等边三角形,则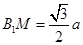 ,又因为面
,又因为面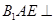 面
面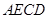 ,所以
,所以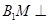 面
面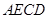 ,
,所以
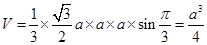 …………4分
…………4分(Ⅱ)连接
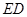 交
交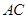 于
于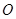 ,连接
,连接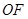 ,因为
,因为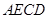 为菱形,
为菱形, ,又
,又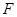 为
为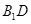 的中点,所以
的中点,所以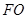 ∥
∥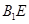 ,所以
,所以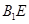 ∥面
∥面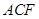 ……………7分
……………7分(Ⅲ)连接
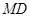 ,分别以
,分别以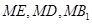 为
为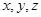 轴
轴则

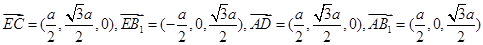 ……9分
……9分设面
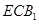 的法向量
的法向量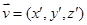 ,
,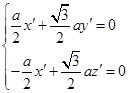 ,令
,令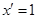 ,则
,则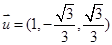
设面
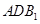 的法向量为
的法向量为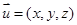 ,
,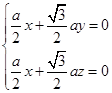 ,令
,令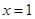 ,则
,则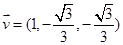 ……11分
……11分则
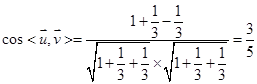 ,所以二面角的余弦值为
,所以二面角的余弦值为
略

练习册系列答案
相关题目
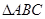 是边长为2的正三角形,俯视图为正六边形,那么该几何体的体积为( )
是边长为2的正三角形,俯视图为正六边形,那么该几何体的体积为( )
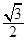
 的内切圆面积为
的内切圆面积为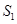 ,外接圆面积为
,外接圆面积为 ,则
,则 ,推广到空间几何中可以得到类似结论:若正四面体
,推广到空间几何中可以得到类似结论:若正四面体 的内切球体积为
的内切球体积为 ,外接球体积为
,外接球体积为 ,则
,则 ( )
( )

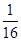

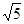 ,BC=AD=
,BC=AD=
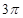 与
与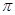 的矩形硬纸卷成圆柱的侧面,则圆柱底面的半径为_
的矩形硬纸卷成圆柱的侧面,则圆柱底面的半径为_  中,
中,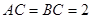 ,
, ,
,  ,点
,点 的中点,
的中点,
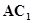 //平面
//平面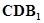 ;
;  的体积.
的体积.
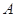 、
、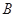 、
、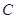 三点,
三点,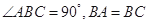 ,球心
,球心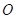 到平面
到平面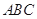 距离是
距离是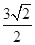 ,则
,则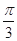
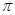
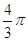
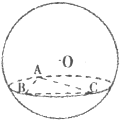
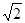 ,
,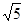 ,
,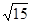 ,试求它的外接球的表面积和体积。
,试求它的外接球的表面积和体积。