题目内容
【题目】求二次函数![]() 分别在下列定义域上的最大值和最小值.
分别在下列定义域上的最大值和最小值.
(1)R;
(2)![]() ;
;
(3)![]() .
.
【答案】(1)![]() ,最小值不存在;(2)
,最小值不存在;(2)![]() ,最小值不存在;(3)答案见解析
,最小值不存在;(3)答案见解析
【解析】
(1)对解析式进行整理可知![]() ,从而可求出最值.
,从而可求出最值.
(2)由函数的对称轴为![]() ,且函数在
,且函数在![]() 上单调递增,即可求出最值.
上单调递增,即可求出最值.
(3) 定义域![]() 是长度为1的可变区间,函数的最值与对称轴
是长度为1的可变区间,函数的最值与对称轴![]() 相对于区间
相对于区间![]() 的位置有关,故分为
的位置有关,故分为![]() ,
,![]() ,
,![]() ,
,![]() 进行讨论,结合抛物线的单调性及图像即可求出最值.
进行讨论,结合抛物线的单调性及图像即可求出最值.
解:(1)∵![]() ,∴
,∴![]() ,且抛物线开口向下,
,且抛物线开口向下,
所以当![]() 时,
时,![]() ,最小值不存在.
,最小值不存在.
(2)由(1)知,![]() 为函数的对称轴,且对称轴
为函数的对称轴,且对称轴![]() ,
,
因为![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
所以当![]() 时,
时,![]() ,最小值不存在.
,最小值不存在.
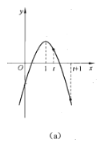
(3)①当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,如图(a)所示.
上单调递减,如图(a)所示.
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
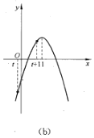
②当![]() 时,即
时,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,如图(b)所示.
上单调递增,如图(b)所示.
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
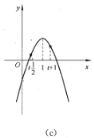
③当![]() 时,
时,![]() 距对称轴比
距对称轴比![]() 距对称轴更远,如图(c)所示.
距对称轴更远,如图(c)所示.
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
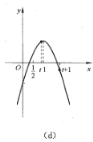
④当![]() 时,
时,![]() 距对称轴比
距对称轴比![]() 距对称轴更远,如图(d)所示.
距对称轴更远,如图(d)所示.
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
综上所述:当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() ;当
;当![]() 时,
时,![]() ,
,![]() .
.

练习册系列答案
相关题目