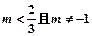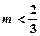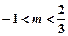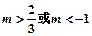题目内容
(本小题满分12分)
已知函数 是定义在
是定义在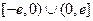 上的奇函数,当
上的奇函数,当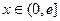 ,
, (其中
(其中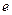 是自然对数的底,
是自然对数的底,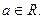 )
)
(1)求 的解析式;
的解析式;
(2)设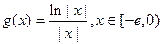 ,求证:当
,求证:当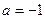 时,
时,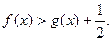
(3)是否存在实数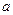 ,使得当
,使得当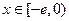 时,
时, 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数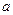 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
已知函数
 是定义在
是定义在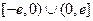 上的奇函数,当
上的奇函数,当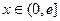 ,
, (其中
(其中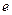 是自然对数的底,
是自然对数的底,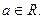 )
)(1)求
 的解析式;
的解析式;(2)设
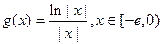 ,求证:当
,求证:当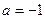 时,
时,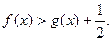
(3)是否存在实数
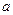 ,使得当
,使得当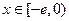 时,
时, 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数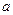 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。(1)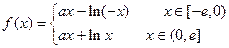
(2)略
(3)存在实数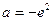 ,使得
,使得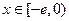 时,
时, 有最小值3
有最小值3
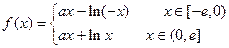
(2)略
(3)存在实数
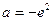 ,使得
,使得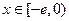 时,
时, 有最小值3
有最小值3解:(1)
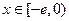 ,则
,则
所以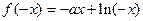
又因为 是
是 定义在
定义在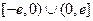 上的奇函数,
上的奇函数,
所以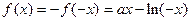 …………2分
…………2分
故函数 的解析式为
的解析式为
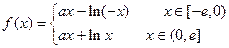 ……3分
……3分
 (2)证明:当
(2)证明:当
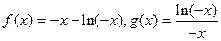
设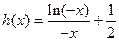
因为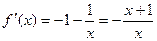
所以当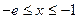 时,
时,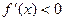
此时 单调递减…………5分
单调递减…………5分
当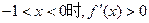 ,此时
,此时 单调递增
单调递增
所以 的最小值为
的最小值为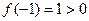
又因为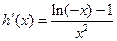
所以当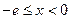 时,
时,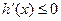 ,此时
,此时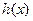 单调递减
单调递减
所以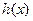 的最大值为
的最大值为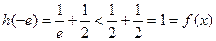 的最小值
的最小值
所以当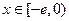 时,
时,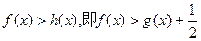 …………8分
…………8分
(3)假设存在实数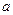 ,使得当
,使得当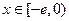 ,时,
,时,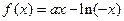 有最小值为3
有最小值为3
则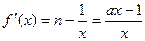 …………9分
…………9分
① 当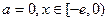 时,
时,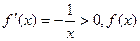 在区间
在区间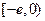 单调递增,
单调递增,
 最小值为
最小值为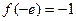 ,不满足最小值是3
,不满足最小值是3
②当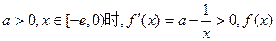 在区间
在区间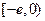 上单调递增,
上单调递增, 的最小值是
的最小值是 ,也不满足最小值3
,也不满足最小值3
③当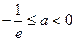 ,
,
故函数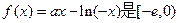 增函数。
增函数。
所以 的最小值为
的最小值为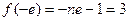 ,解得
,解得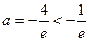 (舍去)
(舍去)
④当 时,
时, ,此时函数
,此时函数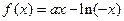
 是减函数
是减函数
当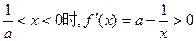 ,
,
此时函数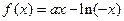 是减函数
是减函数
所以 的最小值为
的最小值为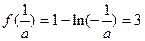 ,解得
,解得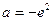 ……611
……611 分
分
综上可知,存在实数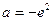 ,使得
,使得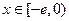 时,
时, 有最小值3…………12分
有最小值3…………12分

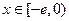 ,则
,则
所以
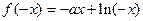
又因为
 是
是 定义在
定义在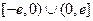 上的奇函数,
上的奇函数,所以
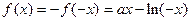 …………2分
…………2分故函数
 的解析式为
的解析式为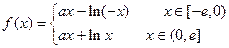 ……3分
……3分 (2)证明:当
(2)证明:当
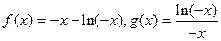
设
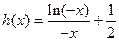
因为
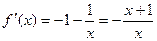
所以当
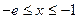 时,
时,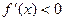
此时
 单调递减…………5分
单调递减…………5分
当
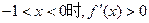 ,此时
,此时 单调递增
单调递增所以
 的最小值为
的最小值为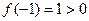
又因为
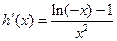
所以当
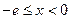 时,
时,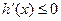 ,此时
,此时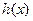 单调递减
单调递减所以
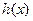 的最大值为
的最大值为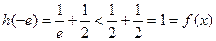 的最小值
的最小值所以当
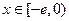 时,
时,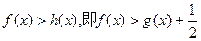 …………8分
…………8分(3)假设存在实数
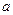 ,使得当
,使得当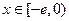 ,时,
,时,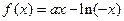 有最小值为3
有最小值为3则
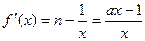 …………9分
…………9分① 当
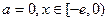 时,
时,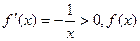 在区间
在区间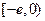 单调递增,
单调递增, 最小值为
最小值为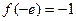 ,不满足最小值是3
,不满足最小值是3②当
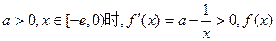 在区间
在区间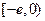 上单调递增,
上单调递增, 的最小值是
的最小值是 ,也不满足最小值3
,也不满足最小值3③当
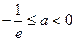 ,
,
故函数
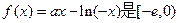 增函数。
增函数。所以
 的最小值为
的最小值为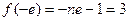 ,解得
,解得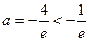 (舍去)
(舍去)④当
 时,
时, ,此时函数
,此时函数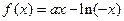
 是减函数
是减函数当
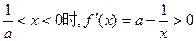 ,
,此时函数
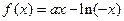 是减函数
是减函数所以
 的最小值为
的最小值为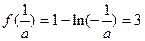 ,解得
,解得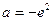 ……611
……611 分
分综上可知,存在实数
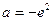 ,使得
,使得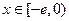 时,
时, 有最小值3…………12分
有最小值3…………12分
练习册系列答案
相关题目
 设备,进行该
设备,进行该 产品的生产加工.已知生产这种产品每件还需成本费40元,经过市场调研发现:该产品的销售单价定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上,每增加10元,年销售量将再减少1万件.设销售单价为
产品的生产加工.已知生产这种产品每件还需成本费40元,经过市场调研发现:该产品的销售单价定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上,每增加10元,年销售量将再减少1万件.设销售单价为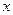 (元),年销售量为
(元),年销售量为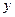 (万件),年获利为
(万件),年获利为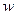 (万元).
(万元). 是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)
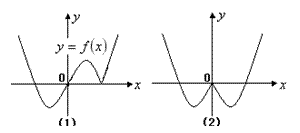
是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)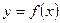 ,则下图(2)中的图像对应的函数在下列给出的四个式子中,只可能是( )
,则下图(2)中的图像对应的函数在下列给出的四个式子中,只可能是( ) 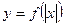
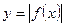
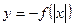
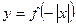
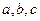 为正数,关于
为正数,关于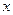 的一元二次方程
的一元二次方程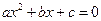 有两个相等的实数根.则方程
有两个相等的实数根.则方程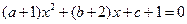 的实数根的个数是( )
的实数根的个数是( )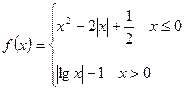 的零点个数为( ).
的零点个数为( ). 个
个 个
个 个
个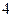 个
个 ( )
( )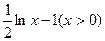
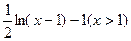
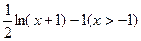
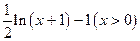
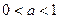 时,在同一坐标系中,函数
时,在同一坐标系中,函数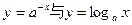 的图象是 ( )
的图象是 ( )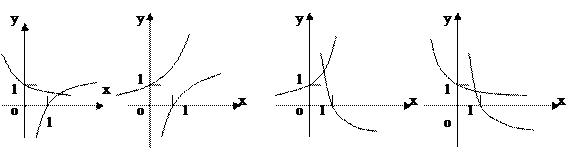 A B C D
A B C D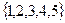 ,B=
,B=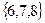 ,从集合A到集合B的映射中,满足
,从集合A到集合B的映射中,满足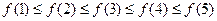 的映射有 ( )
的映射有 ( ) 函数
函数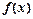 是定义在R上的奇函数,若
是定义在R上的奇函数,若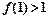 ,
,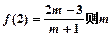 的取值范围是( )
的取值范围是( )