题目内容
【题目】已知函数
，
（
）.
（1）若
，求
在
上的最小值；
（2）若
对于任意的实数
恒成立，求
的取值范围；
（3）当
时，求函数
在
上的最小值.
【答案】（1）
；（2）
；（3）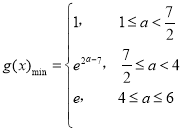
.
【解析】
（1）利用基本不等式求解最值；
（2）转化为
对于任意的实数x恒成立，求参数的取值范围；
（3）函数去绝对值，等价转化为比较
与
的大小关系，数形结合求解.
（1）对于
，
，
所以
，
当且仅当
，即
时等号成立，所以.
（2）
对于任意的实数x恒成立，即
对于任意的实数x恒成立，亦即
对于任意的实数x恒成立，
所以
，即对于任意的实数x恒成立.
又
对于任意的实数x恒成立，
故只需
，解得
，所以
的取值范围为.
（3）
，
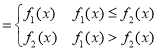因为
与
的底数都同为e，外函数都单调递增，
所以，比较与的大小关系，只须比较与的大小关系.
令
，
，
，其中
，
.
因为，所以
.
令
，得
，由题意可得如下图象：
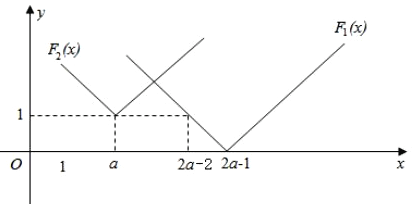
（i）当
，即
时，
，
；
（ii）当
，即
时，
，
；
（iii）当
，即
时，
，
；
综上所述，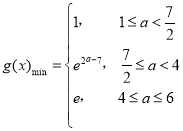
.
练习册系列答案
名校课堂系列答案
相关题目
