Question

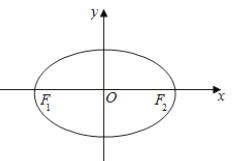
【题目】已知， 为椭圆： 的左、右焦点，点在椭圆上，且面积的最大值为．

（Ⅰ）求椭圆的方程；

（Ⅱ）若直线与椭圆交于， 两点， 的面积为1， （， ），当点在椭圆上运动时，试问是否为定值？若是定值，求出这个定值；若不是定值，求出的取值范围．

Answer 1

【答案】（I）；（II）为定值.

【解析】试题分析：

(1)利用题意求得，即有椭圆的方程为．

(2)利用题意联立直线与椭圆的方程，设而不求可得为定值．

试题解析：（Ⅰ）由题意得，

当为短轴端点时， 面积取得最大值，

解得， ，

即有椭圆的方程为．

（Ⅱ）设直线的方程为，代入椭圆方程，

可得，

设， ，

即有， ，

，

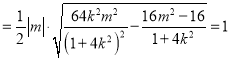化简可得．

设，由，可得， ．

又因为点在椭圆上，所以有，

整理可得： ，

即为．

由， ，

可得

，

可得，即有为定值．