题目内容
已知函数 (
(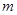 为常数,
为常数, ),且数列
),且数列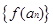 是首项为
是首项为 ,公差为
,公差为 的等差数列.
的等差数列.
(1) 若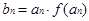 ,当
,当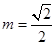 时,求数列
时,求数列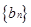 的前
的前 项和
项和 ;
;
(2)设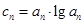 ,如果
,如果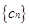 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求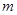 的取值范围.
的取值范围.
(1) 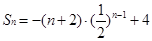 (2)
(2) 
解析试题分析:(1) 由题意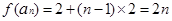 ,即
,即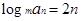 , 1分
, 1分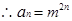 . ……2分
. ……2分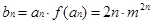 ,
,
当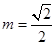 时,
时,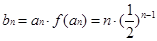 . 3分
. 3分
∴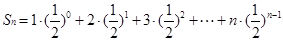 , ①
, ① 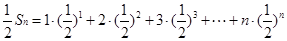 ② 4分
② 4分
①-②,得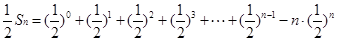
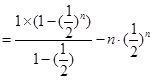 6分
6分
∴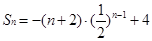 7分
7分
(2)由(1)知,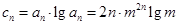 ,要使
,要使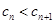 对一切
对一切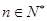 成立,
成立,
即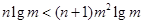 对一切
对一切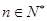 成立. ……8分
成立. ……8分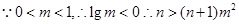 ,对一切
,对一切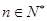 恒成立,
恒成立,
只需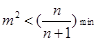 , 10分
, 10分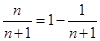 单调递增,∴当
单调递增,∴当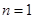 时,
时,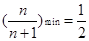 . 12分
. 12分
∴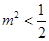 ,且
,且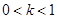 , ∴
, ∴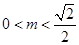 . 13分
. 13分
综上所述,存在实数 满足条件. 14分
满足条件. 14分
考点:本题考查了数列的求和及不等式的证明
点评:数列的通项公式及应用是数列的重点内容,数列的大题对逻辑推理能力有较高的要求,在数列中突出考查学生的理性思维,这是近几年新课标高考对数列考查的一个亮点,也是一种趋势.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
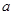 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少? (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元. 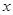 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,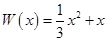 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,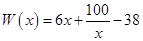 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.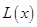 (万元)关于年产量
(万元)关于年产量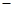 固定成本
固定成本

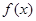 有两个零点
有两个零点 和
和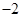 ,且
,且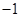 ,函数
,函数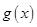 与
与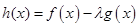 在区间
在区间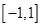 上是增函数,求实数
上是增函数,求实数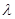 的取值范围。
的取值范围。 ,若
,若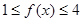 对一切
对一切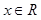 恒成立.求实数
恒成立.求实数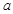 的取值范围.(16分)
的取值范围.(16分)