题目内容
设数列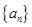 为等差数列,且
为等差数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,
, 且
且 .
.
(1)求数列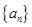 ,
, 的通项公式;
的通项公式;
(2)若 ,
, 为数列
为数列 的前
的前 项和,
项和, 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.
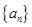 为等差数列,且
为等差数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,
, 且
且 .
.(1)求数列
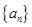 ,
, 的通项公式;
的通项公式;(2)若
 ,
, 为数列
为数列 的前
的前 项和,
项和, 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.(1)  ,
, ;(2)m的最小值是
;(2)m的最小值是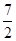 .
.
 ,
, ;(2)m的最小值是
;(2)m的最小值是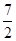 .
.试题分析:(1)确定数列
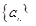 为的公差
为的公差 ,
, ,即得
,即得 ,
,由已知得
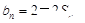 ,当
,当 时,得
时,得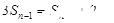 ,
, 两式相减整理得
 ,所以
,所以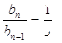
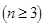 又
又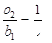 ,得知
,得知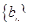 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.(2)
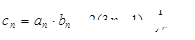
利用“错位相减法” 求和
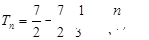 ,
,从而

为使
 对
对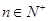 恒成立,得到
恒成立,得到 ,确定m的最小值是
,确定m的最小值是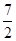 .
.解得本题的关键是确定数列的基本特征.
(1) 数列
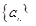 为等差数列,公差
为等差数列,公差 ,易得
,易得 ,
,所以
 1分
1分由
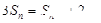 ,得
,得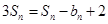 ,即
,即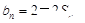 ,
,所以
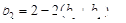 ,又
,又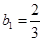 ,所以
,所以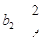 ,
,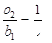 2分
2分由
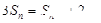 , 当
, 当 时,得
时,得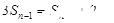 ,
, 两式相减得:
 ,即
,即 ,所以
,所以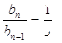
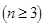 4分
4分又
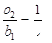 ,所以
,所以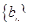 是以
是以 为首项,
为首项, 为公比的等比数列,于是
为公比的等比数列,于是 5分
5分(2)
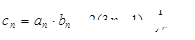
∴
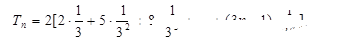 6分
6分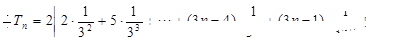 8分
8分两式相减得
 9分
9分所以
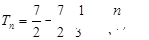 11分
11分从而

∵
 对
对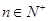 恒成立,∴
恒成立,∴ ∴m的最小值是
∴m的最小值是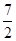 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的各位数字之和等于7,那么称
的各位数字之和等于7,那么称 若
若 ,则
,则 _________.
_________.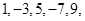 ……的一个通项公式为( )
……的一个通项公式为( )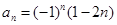
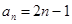
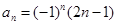
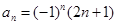
 的通项公式为
的通项公式为 ,则
,则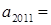 ;
;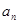 }中,
}中,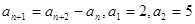 ,则
,则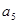 为___________.
为___________.