题目内容
已知等比数列an=
,其前n项和为Sn=
ak,则Sk+1与Sk的递推关系不满足( )
| 1 |
| 3n-1 |
| n |
 |
| k-1 |
A.Sk+1=Sk+
| B.Sk+1=1+
| ||||
| C.Sk+1=Sk+ak+1 | D.Sk+1=3Sk-3+ak+ak+1 |
∵等比数列an=
=31-n,
∴a1=1,a2=
,q=
,
∴Sn=
ak=
=
(1-
),
∴Sk+1=Sk+
,故A不成立;
Sk+1=
(1-
)=
-
×
=1+
-
×
=1+
(1-
)=1+
Sk,故B成立;
由数列的前n项和的定义知:Sk+1=Sk+ak+1,故C成立;
∵3Sk-3+ak+ak+1
=3×
(1-
)-3+31-k+3-k
=
-
×
-3+
+
=
-
×
=
(1-
)=Sk+1,故D成立.
故选A.
| 1 |
| 3n-1 |
∴a1=1,a2=
| 1 |
| 3 |
| 1 |
| 3 |
∴Sn=
| n |
 |
| k=1 |
1-
| ||
1-
|
| 3 |
| 2 |
| 1 |
| 3n |
∴Sk+1=Sk+
| 1 |
| 3k |
Sk+1=
| 3 |
| 2 |
| 1 |
| 3n |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3n |
=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3n-1 |
=1+
| 1 |
| 2 |
| 1 |
| 3n-1 |
| 1 |
| 3 |
由数列的前n项和的定义知:Sk+1=Sk+ak+1,故C成立;
∵3Sk-3+ak+ak+1
=3×
| 3 |
| 2 |
| 1 |
| 3k-1 |
=
| 9 |
| 2 |
| 9 |
| 2 |
| 1 |
| 3n-1 |
| 1 |
| 3k-1 |
| 3 |
| 3k-1 |
=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3k-1 |
=
| 3 |
| 2 |
| 1 |
| 3k |
故选A.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目

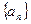 中,
中,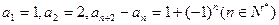 ,则
,则