题目内容
【题目】已知等差数列{an}满足a2=2,a5=8.
(1)求{an}的通项公式;
(2)各项均为正数的等比数列{bn}中,b1=1,b2+b3=a4,求{bn}的前n项和Tn.
【答案】(1)an=2n-2.(2)Tn=2n-1.
【解析】试题分析:(1)将已知条件转化为首项和公差表示,解方程组求得基本量,即可得到通项公式;(2)由b1=1,b2+b3=a4,解方程组可得到等比数列{bn}的首项和公比,代入公式可求得前n项和
试题解析:(1)设等差数列{an}的公差为d,
则由已知得![]() ∴a1=0,d=2.
∴a1=0,d=2.
∴an=a1+(n-1)d=2n-2.
(2)设等比数列{bn}的公比为q,则由已知得q+q2=a4,
∵a4=6,∴q=2或q=-3.
∵等比数列{bn}的各项均为正数,∴q=2.
∴{bn}的前n项和Tn=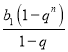 =
=![]()
=2n-1.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】(本题满分12分)为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图:
组别 | 锻炼次数 | 频数(人) | 频率 |
1 |
| 2 | 0.04 |
2 |
| 11 | 0.22 |
3 |
| 16 |
|
4 |
| 15 | 0.30 |
5 |
|
|
|
6 |
| 2 | 0.04 |
[ | 合计 |
| 1.00 |

(1)求频率分布表中![]() 、
、![]() 、
、![]() 及频率分布直方图中
及频率分布直方图中![]() 的值;
的值;
(2)求参加锻炼次数的众数(直接写出答案,不要求计算过程);
(3)若参加锻炼次数不少于18次为及格,估计这次体育锻炼的及格率。
【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大。某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户按年龄分组进行访谈,统计结果如下表.
组号 | 年龄 | 访谈人数 | 愿意使用 |
1 | [20,30) | 5 | 5 |
2 | [30.40) | 10 | 10 |
3 | [40.50) | 15 | 12 |
4 | [50.60) | 14 | 8 |
5 | [60,70) | 6 | 2 |
(1)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取15人,则各组应分别抽取多少人?
(2)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(3)按以上统计数据填写下面2×2列联表,并判断以50岁为分界点,能否在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关;
年龄不低于50岁的人数 | 年龄低于50岁的人数 | 合计 | |||||
愿意使用的人数 | |||||||
不愿意使用的人数 | |||||||
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |