题目内容
已知数列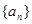 中各项均为正数,
中各项均为正数,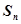 是数列
是数列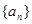 的前
的前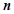 项和,且
项和,且
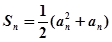 .
.
(1)求数列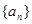 的通项公式
的通项公式
(2)对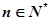 ,试比较
,试比较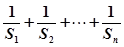 与
与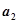 的大小.
的大小.
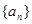 中各项均为正数,
中各项均为正数,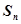 是数列
是数列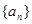 的前
的前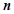 项和,且
项和,且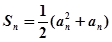 .
.(1)求数列
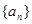 的通项公式
的通项公式 (2)对
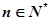 ,试比较
,试比较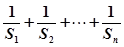 与
与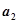 的大小.
的大小. (1)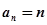 ,(
,(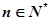 )(2)
)(2)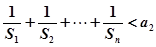
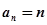 ,(
,(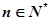 )(2)
)(2)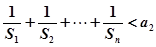
不能使主要是考查了数列的通项公式与其前n项和的关系式的运用,以及裂项法求和的综合运用
(1)根据对于n分为两种情况讨论得到其通项公式 。
(2)由一问中知道数列的通项公式,那么得到Sn,然后根据通项公式的特点裂项得到和式。
解: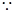
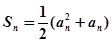 ,
, 当
当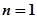 时,
时,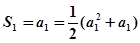 ,又
,又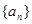 中各项均为正数解得
中各项均为正数解得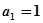 ,………………………2分
,………………………2分
当 时,
时, 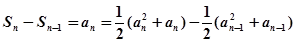 ………………………4分
………………………4分

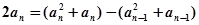 ,即
,即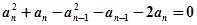
即 ,
,
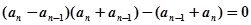

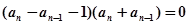 ,
,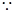
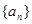 中各项均为正数,
中各项均为正数,

即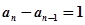 (
( ),
),
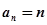 ,(
,( ),………………………6分
),………………………6分
又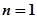 时,
时,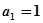 ,
, 数列
数列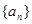 的通项公式是
的通项公式是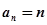 ,(
,(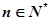 ). …………8分
). …………8分
(2) 对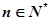 ,
,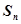 是数列
是数列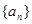 的前
的前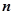 项和,
项和,

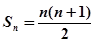 ,
,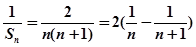 ………………10分
………………10分

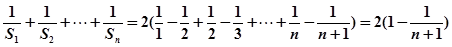 …12分
…12分
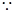
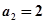 ,
,
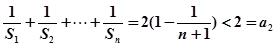

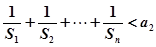 …………14分
…………14分
(1)根据对于n分为两种情况讨论得到其通项公式 。
(2)由一问中知道数列的通项公式,那么得到Sn,然后根据通项公式的特点裂项得到和式。
解:
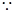
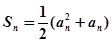 ,
, 当
当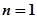 时,
时,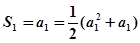 ,又
,又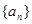 中各项均为正数解得
中各项均为正数解得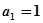 ,………………………2分
,………………………2分当
 时,
时, 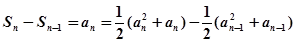 ………………………4分
………………………4分
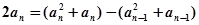 ,即
,即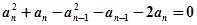
即
 ,
,
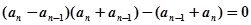

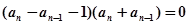 ,
,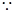
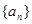 中各项均为正数,
中各项均为正数,

即
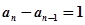 (
( ),
),
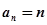 ,(
,( ),………………………6分
),………………………6分又
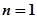 时,
时,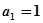 ,
, 数列
数列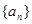 的通项公式是
的通项公式是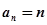 ,(
,(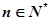 ). …………8分
). …………8分(2) 对
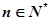 ,
,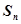 是数列
是数列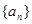 的前
的前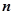 项和,
项和,
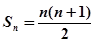 ,
,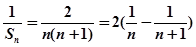 ………………10分
………………10分
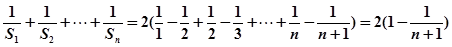 …12分
…12分
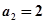 ,
,
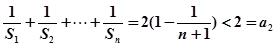

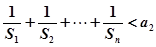 …………14分
…………14分
练习册系列答案
相关题目
 的前
的前 项和为
项和为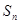 ,且
,且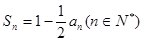
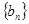 的通项公式
的通项公式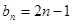 ,记
,记 ,求数列
,求数列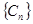 的前
的前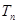 .
.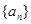 的前
的前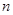 项和为
项和为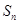 ,已知
,已知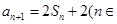 N
N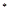 ).
).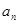 与
与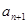 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为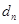 的等差数列,求数列
的等差数列,求数列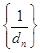 的前
的前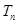 .(6分)
.(6分)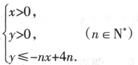 表示的平面区域为
表示的平面区域为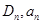 表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则
表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则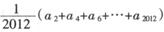 =( )
=( )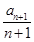 =
=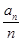 +
+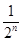 .
.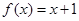 ,设
,设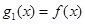 ,
,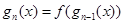
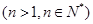 .
. 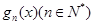 的表达式;此时若设
的表达式;此时若设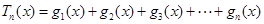 ,且关于
,且关于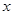 的函数
的函数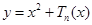
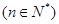 在区间
在区间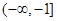 上的最小值为
上的最小值为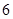 ,则求
,则求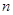 的值;
的值;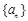 为等比数列,数列
为等比数列,数列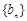 满足
满足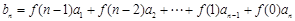 ,
,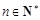 ,若
,若 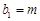 ,
,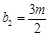 ,其中
,其中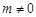 ,则
,则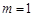 时,求
时,求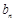 ;
;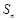 为数列
为数列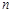 项和,若对于任意的正整数
项和,若对于任意的正整数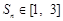 ,求实数
,求实数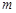 的取值范围.
的取值范围.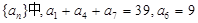 则数列
则数列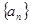 的前9项的和
的前9项的和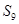 等于()
等于()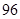
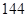
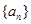 中,若
中,若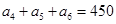 ,则
,则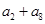 的值为 .
的值为 .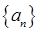 的前n项和为
的前n项和为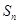 ,且
,且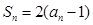 ,则
,则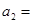 _______.
_______.