题目内容
4.不论m为何值,直线(3m+4)x+(5-2m)y+7m-6=0都恒过一定点,则此定点的坐标是(-1,2).分析 直线的方程可化为:(3x-2y+7)m+(4x+5y-6)=0,不论m为何实数,直线l恒过直线3x-2y+7=0和4x+5y-6=0的交点,解方程组求得坐标.
解答 解:直线L的方程可化为:(3x-2y+7)m+(4x+5y-6)=0
令:3x-2y+7=0且4x+5y-6=0
解得:x=-1,y=2,
∴直线恒过定点(-1,2).
故答案为:(-1,2).
点评 本题主要考查直线过定点问题,令参数m的系数等于零,求得x和y的值,即可得到定点的坐标,属于基础题.

练习册系列答案
相关题目
9.已知f(x)为R上的增函数,则满足f($\frac{1}{x}$)<f(1)的实数x的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,0)∪(0,1) | D. | (-∞,0)∪(1,+∞) |
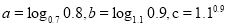 ,则
,则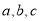 的大小关系是( )
的大小关系是( )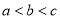 B.
B.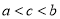
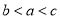 D.
D.