题目内容
1.已知公差不为0的等差数列{an}中,a2,a3,a5成等比数列,a1+a2=1.(I)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=$\frac{1}{{a}_{n+1}{a}_{n+3}}$,n∈N*,求数列{bn}的前n项和Tn.
分析 (I)利用等差数列与等比数列的通项公式及其性质即可得出;
(II)bn=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,利用“裂项求和”即可得出.
解答 解:(I)设等差数列{an}的公差为d≠0,
∵a2,a3,a5成等比数列,∴${a}_{3}^{2}$=a2a5,
又a1+a2=1.
联立可得$\left\{\begin{array}{l}{({a}_{1}+2d)^{2}=({a}_{1}+d)({a}_{1}+4d)}\\{2{a}_{1}+d=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=0}\\{d=1}\end{array}\right.$,
∴an=0+(n-1)×1=n-1.
(II)bn=$\frac{1}{{a}_{n+1}{a}_{n+3}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴数列(bn}的前n项和Tn=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})$+$(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$
=$\frac{3}{4}$-$\frac{2n+3}{2{n}^{2}+6n+4}$.
点评 本题考查了等差数列与等比数列的通项公式及其性质、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

| A. | 990 | B. | 1000 | C. | 1100 | D. | 99 |
| A. | (-6,6) | B. | [-6,6] | C. | (-∞,-6]∪[6,+∞) | D. | (-∞,-6)∪(6,+∞) |
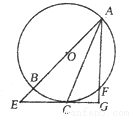
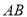 过圆心
过圆心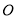 ,交圆
,交圆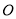 于
于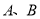 ,直线
,直线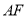 交圆
交圆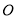 于
于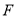 (不与
(不与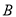 重合),直线
重合),直线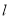 与圆
与圆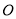 相切于
相切于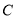 ,交
,交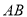 于
于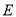 ,且与
,且与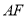 垂直,垂足为
垂直,垂足为 ,连接
,连接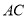 .
.
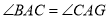 ;
;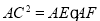 .
. ,若存在实数
,若存在实数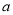 ,使得
,使得 ,则
,则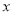 的取值范围为( )
的取值范围为( ) B.
B.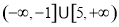
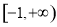 D.
D.