题目内容
16.复数z=a+2i1+ia+2i1+i+(3-i),若z为纯虚数.则实数a的值为-8.分析 首先进行复数的除法运算,分子和分母同乘以分母的共轭复数,整理成复数的标准形式,根据复数是一个纯虚数,得的复数的实部等于0,而虚部不等于0,得的a的值
解答 解:z=a+2i1+ia+2i1+i+(3-i)=(a+2i)(1−i)(1+i)(1−i)+(3-i)=a+22+3+(2−a2-1)i,
∵z为纯虚数,
∴a+22+3=0,2−a2-1≠0
解得a=-8,
故答案为:-8.
点评 本题考查复数的代数形式的乘除运算,考查复数的基本概念,在计算过程中,注意复数的代数形式的除法的运算法则,注意纯虚数的实部为零,而虚部不为0.

练习册系列答案
相关题目
11.函数y=3x2+ax+4在区间[-1,1]上不是单调函数,则实数a的取值范围是( )
| A. | (-6,6) | B. | [-6,6] | C. | (-∞,-6]∪[6,+∞) | D. | (-∞,-6)∪(6,+∞) |

 过圆心
过圆心 ,交圆
,交圆 于
于 ,直线
,直线 交圆
交圆 于
于 (不与
(不与 重合),直线
重合),直线 与圆
与圆 相切于
相切于 ,交
,交 于
于 ,且与
,且与 垂直,垂足为
垂直,垂足为 ,连接
,连接 .
.
 ;
; .
. .
.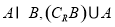 ;
; ,若
,若 ,求实数
,求实数 的取值集合.
的取值集合.