题目内容
【题目】已知二次函数f(x)=ax2+bx+c.
(1)若f(﹣1)=0,f(0)=0,求出函数f(x)的零点;
(2)若f(x)同时满足下列条件:①当x=﹣1时,函数f(x)有最小值0,②f(1)=1求函数f(x)的解析式;
(3)若f(1)≠f(3),证明方程f(x)= ![]() [f(1)+f(3)]必有一个实数根属于区间(1,3)
[f(1)+f(3)]必有一个实数根属于区间(1,3)
【答案】
(1)解:∵f(﹣1)=0,f(0)=0,
∴a=b;
∴f(x)=ax(x+1);
∴函数f(x)的零点是0和﹣1
(2)解:由条件①得: ![]() ,a>0;
,a>0;
∴b=2a,b2=4ac,
∴4a2=4ac,
∴a=c;
由条件②知:a+b+c=1,
由 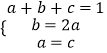 解得,
解得,
![]() .
.
∴ ![]()
(3)证明:令 ![]() ,
,
则 ![]() ,
,
![]() ,
,
∴ ![]() ,
,
∴g(x)=0在(1,3)内必有一个实根,
即方程 ![]() 必有一个实数根属于(1,3).
必有一个实数根属于(1,3).
【解析】(1)由f(﹣1)=0,f(0)=0得a=b;从而化简f(x)=ax(x+1);从而确定零点;(2)由条件化简可得方程 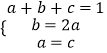 ,从而解得;(3)令
,从而解得;(3)令 ![]() ,从而可判断
,从而可判断 ![]() ,从而证明
,从而证明

练习册系列答案
相关题目