题目内容
6.已知函数f(x)=x3-ax2-3x,g(x)=-6x(a∈R).(Ⅰ)若x=3是d的极值点,求f(x)在[1,a]上的最小值和最大值;
(Ⅱ)若h(x)=f(x)-g(x)在x∈(0,+∞)时是增函数,求实数a的取值范围.
分析 (I)求出函数f(x)的导数,由题意得f′(3)=0,解方程可得a=4,求得[1,4]上函数f(x)的单调区间,即可得到最值;
(II)求得h(x)的解析式和导数,由题意得,h′(x)≥0在(0,+∞)恒成立,由参数分离和基本不等式,即可得到a的范围.
解答 解:(I)f′(x)=3x2-2ax-3,
由题意得f′(3)=0,即27-6a-3=0,
解得a=4,
f′(x)=3x2-8x-3=3(x-3)(x+$\frac{1}{3}$),
当x∈(1,3),f′(x)<0,f(x)单调递减,
当x∈(3,4),f′(x)>0,f(x)单调递增,
即有f(x)在[1,4]上的最大值为f(1)=-6,最小值为f(3)=-18;
(II)h(x)=f(x)-g(x)=x3-ax2+3x,
由题意得,h′(x)=3x2-2ax+3≥0在(0,+∞)恒成立,
即$a≤\frac{3}{2}({x+\frac{1}{x}})$在(0,+∞)恒成立,
而${({x+\frac{1}{x}})_{min}}=2$,
所以a≤3.
则实数a的取值范围为(-∞,3].
点评 本题考查导数的运用:求单调区间和极值、最值,主要考查不等式恒成立问题转化为求函数的最值问题,考查运算能力,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
12.如图,正方形A1BCD折成直二面角A-BD-C,则二面角A-CD-B的余弦值是( )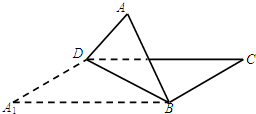

| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
9.已知函数f(x)=2|xsinx|,则函数f(x)在区间[-2π,2π]上的零点个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |