Question

【题目】已知函数.

（1）讨论函数的单调性；

（2）若不等式在时恒成立，求实数的取值范围；

（3）当时，证明： ．

Answer 1

【答案】（1）见解析；（2）；（3）见解析

【解析】分析：（1）求出的导函数，由得增区间，由得减区间，注意在解不等式时要按的值分类讨论；

（2）由（1）的结论知当时，，题中不等式成立，而当时，题中不等式不恒成立；

（3）时，由（2）知上有，从而，令，然后所有不等式相加可证．

详解： (1)∵y＝f(x)－g(x)＝ln(ax＋1)－，

y′＝－＝，

当a≥1时，y′≥0，所以函数y＝f(x)－g(x)是[0，＋∞)上的增函数；

当0<a<1时，由y′>0得x>2，所以函数y＝f(x)－g(x)在上是单调递增函数，函数y＝f(x)－g(x)在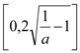上是单调递减函数；

(2)当a≥1时，函数y＝f(x)－g(x)是[0，＋∞)上的增函数．

所以f(x)－g(x)≥f(0)－g(0)＝1，

即不等式f(x)≥g(x)＋1在x∈[0，＋∞)时恒成立，

当0<a<1时，函数y＝f(x)－g(x)是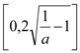上的减函数，存在，使得f(x0)－g(x0)<f(0)－g(0)＝1，即不等式f(x0)≥g(x0)＋1不成立，

综上，实数a的取值范围是[1，＋∞)．

(3)当a＝1时，由(2)得不等式f(x)>g(x)＋1在x∈(0，＋∞)时恒成立，

即ln(x＋1)>，所以，

即< [ln(k＋1)－lnk]．

所以< (ln2－ln1)，

< (ln3－ln2)，

< (ln4－ln3)，…，

< [ln(n＋1)－lnn]．

将上面各式相加得到，＋＋＋…＋< [(ln2－ln1)＋(ln3－ln2)＋(ln4－ln3)＋…＋(ln(n＋1)－lnn)]＝ln(n＋1)＝f(n)．

∴原不等式成立．