题目内容
【题目】旅行社为去广西桂林的某旅游团包飞机去旅游，其中旅行社的包机费为10000元，旅游团中的每人的飞机票按以下方式与旅行社结算：若旅游团的人数在20或20以下，飞机票每人收费800元；若旅游团的人数多于20，则实行优惠方案，每多1人，机票费每张减少10元，但旅游团的人数最多为75，则该旅行社可获得利润的最大值为（ ）
A. 12000元B. 15000元C. 12500元D. 20000元
【答案】B
【解析】
设旅游团的人数为
，每张机票为
元，该旅行社可获得利润为
元，利用一次函数和二次函数的性质，分别求出当
时和当
时，的最大值即可.
设旅游团的人数为，每张机票为元，该旅行社可获得利润为元，
当时，
，
，显然当
时，有最大值，最大值为
；
当时，
，
，
显然当
时，有最大值，最大值为
，故本题选B.
练习册系列答案
名校课堂系列答案
相关题目
【题目】某百货公司1～6月份的销售量
与利润
的统计数据如下表：
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x（万件） | 10 | 11 | 13 | 12 | 8 | 6 |
利润y（万元） | 22 | 25 | 29 | 26 | 16 | 12 |
附：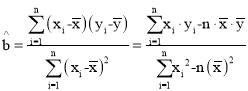
（1）根据2～5月份的统计数据，求出关于的回归直线方程
（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过
万元，则认为得到的回归直线方程是理想的，试问所得回归直线方程是否理想？（参考公式：，
）
