Question

【题目】如图，在四面体中，，点分别是的中点．

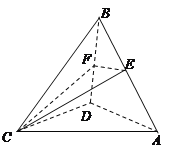
求证：（1）直线平面；

（2）平面平面．

Answer 1

【答案】证明：（1）∵E,F分别是的中点．

∴EF是△ABD的中位线，∴EF∥AD，

∵EF∥面ACD，AD面ACD，∴直线EF∥面ACD；

（2）∵AD⊥BD，EF∥AD，∴EF⊥BD，

∵CB=CD，F是ＢＤ的中点，∴CF⊥BD

又EF∩CF="F, " ∴BD⊥面EFC，

∵BD面BCD，∴面面

【解析】

试题分析：（1）根据线面平行关系的判定定理，在面ACD内找一条直线和直线EF平行即可，根据中位线可知EF∥AD，EF面ACD，AD面ACD，满足定理条件；（2）需在其中一个平面内找一条直线和另一个面垂直，由线面垂直推出面面垂直，根据线面垂直的判定定理可知BD⊥面EFC，而BD面BCD，满足定理所需条件．

解析：

（1）∵E，F分别是AB，BD的中点．

∴EF是△ABD的中位线，∴EF∥AD，

∵EF面ACD，AD面ACD，∴直线EF∥面ACD；

（2）∵AD⊥BD，EF∥AD，∴EF⊥BD，

∵CB=CD，F是BD的中点，∴CF⊥BD

又EF∩CF=F，∴BD⊥面EFC，

∵BD面BCD，∴面EFC⊥面BCD