题目内容
16.（本小题满分8分）直线l过直线x + y－2 = 0和直线x－y + 4 = 0的交点，且与直线3x－2y + 4 = 0平行，求直线l的方程.
解法一：联立方程：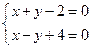
解得
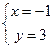，即直线l过点(－1,3)，
由直线l与直线3x－2y + 4 = 0平行得：直线l的斜率为，
所以直线l的方程为：y－3 = (x + 1) 即3x－2y + 9 = 0.
解法二：∵直线x + y－2 = 0不与3x－2y + 4 = 0平行
∴可设符合条件的直线l的方程为：x－y + 4 + λ(x + y－2)= 0
整理得：(1 + λ)x + (λ－1)y + 4－2λ = 0
∵直线l与直线3x－2y + 4 = 0平行
∴ 解得λ =
∴直线l的方程为：x－y + = 0即3x－2y + 9 = 0
解析
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
与两坐标轴围成的三角形的面积为3，分别求满足下列条件的直线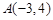
.
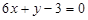垂直.
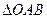的顶点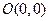
、
、
，
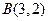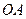边上的中线所在直线为
.
关于直线
的交点且平行于直线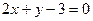
的直线方程. （8分）
内有一点P（2，2），过点P作直线l交圆C于A、B两点.
,求圆的方程.
：x+my+m=0