题目内容
已知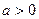 ,函数
,函数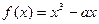 ,在
,在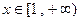 是一个单调函数。
是一个单调函数。
(1)试问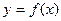 在
在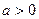 的条件下,在
的条件下,在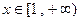 能否是单调递减函数?说明理由。
能否是单调递减函数?说明理由。
(2)若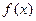 在
在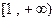 上是单调递增函数,求实数a的取值范围。
上是单调递增函数,求实数a的取值范围。
(3)设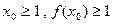 且
且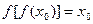 ,比较
,比较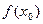 与
与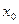 的大小。
的大小。
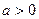 ,函数
,函数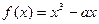 ,在
,在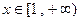 是一个单调函数。
是一个单调函数。(1)试问
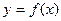 在
在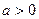 的条件下,在
的条件下,在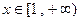 能否是单调递减函数?说明理由。
能否是单调递减函数?说明理由。(2)若
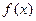 在
在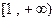 上是单调递增函数,求实数a的取值范围。
上是单调递增函数,求实数a的取值范围。(3)设
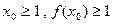 且
且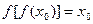 ,比较
,比较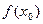 与
与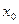 的大小。
的大小。(Ⅰ)略 (Ⅱ)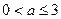 (Ⅲ)
(Ⅲ)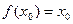
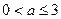 (Ⅲ)
(Ⅲ)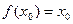
(1)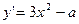 若
若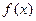 在
在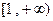 递减,则
递减,则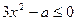 即
即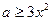 在
在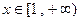 恒成立
恒成立
这样的实数a不存在 ∴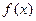 不可能在
不可能在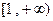 递减
递减
(2)若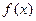 在
在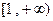 递增,则
递增,则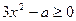 即
即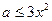 在
在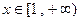 恒成立∴
恒成立∴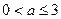
(3)由(1)(2)知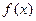 在
在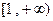 只可能单调递增
只可能单调递增
设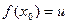 ,则
,则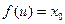 ∴
∴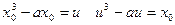
二式相减得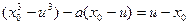 ∴
∴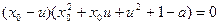
∵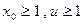 ∴
∴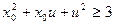 又
又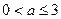 ∴
∴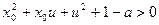
∴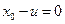 即
即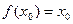
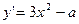 若
若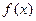 在
在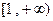 递减,则
递减,则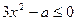 即
即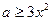 在
在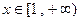 恒成立
恒成立这样的实数a不存在 ∴
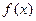 不可能在
不可能在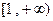 递减
递减(2)若
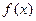 在
在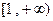 递增,则
递增,则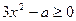 即
即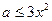 在
在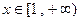 恒成立∴
恒成立∴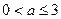
(3)由(1)(2)知
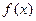 在
在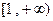 只可能单调递增
只可能单调递增设
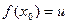 ,则
,则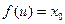 ∴
∴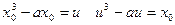
二式相减得
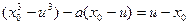 ∴
∴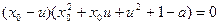
∵
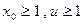 ∴
∴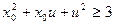 又
又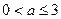 ∴
∴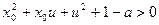
∴
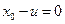 即
即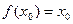

练习册系列答案
相关题目
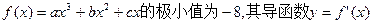
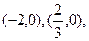 如图所示, (Ⅰ)求
如图所示, (Ⅰ)求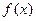 的解析式;
的解析式;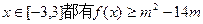 恒成立,
恒成立,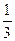 x3+ax2+5x+6在区间[1,3]上为单调函数,则实数a的取值范围为 ( )
x3+ax2+5x+6在区间[1,3]上为单调函数,则实数a的取值范围为 ( ) ,+∞]
,+∞]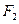 为圆心,过另一焦点
为圆心,过另一焦点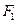 的圆被右准线截的两段弧长之比2:1,
的圆被右准线截的两段弧长之比2:1,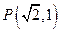 为此平面上一定点,且
为此平面上一定点,且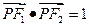 .(1)求椭圆的方程(2)若直线
.(1)求椭圆的方程(2)若直线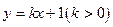 与椭圆交于如图两点A、B,令
与椭圆交于如图两点A、B,令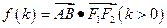 。求函数
。求函数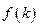 的值域
的值域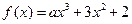 ,若
,若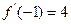 ,则
,则 的值是 。
的值是 。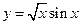 导数为( )
导数为( )



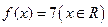 ,则
,则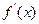 = 。
= 。