题目内容
设f(x)=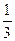 x3+ax2+5x+6在区间[1,3]上为单调函数,则实数a的取值范围为 ( )
x3+ax2+5x+6在区间[1,3]上为单调函数,则实数a的取值范围为 ( )
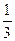 x3+ax2+5x+6在区间[1,3]上为单调函数,则实数a的取值范围为 ( )
x3+ax2+5x+6在区间[1,3]上为单调函数,则实数a的取值范围为 ( )A.[- ,+∞] ,+∞] | B.(-∞ ,-3) |
C.(-∞ ,-3)∪[- ,+∞] ,+∞] | D.[- , , ] ] |
C;
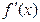 =x2+2ax+5,则f(x)在[1,3]上单调减时,由
=x2+2ax+5,则f(x)在[1,3]上单调减时,由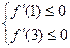 ,得a≤-3;
,得a≤-3; 

当f(x)在[1,3]上单调增时,
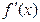 =0中,⊿=4a2-4×5≤0,或
=0中,⊿=4a2-4×5≤0,或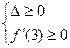 ,
,得a∈[-
 ,
, ]∪[
]∪[ ,+∞].
,+∞]. 综上:a的取值范围是(-∞ ,-3)∪[-
 ,+∞],故选C.
,+∞],故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
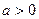 ,函数
,函数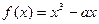 ,在
,在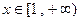 是一个单调函数。
是一个单调函数。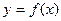 在
在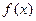 在
在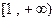 上是单调递增函数,求实数a的取值范围。
上是单调递增函数,求实数a的取值范围。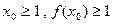 且
且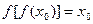 ,比较
,比较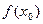 与
与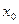 的大小。
的大小。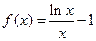 .
.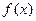 的单调性;
的单调性;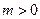 ,求
,求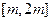 上的最大值;
上的最大值;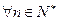 ,不等式
,不等式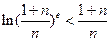 恒成立.
恒成立.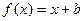 的图像与函数
的图像与函数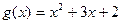 的图象相切,记
的图象相切,记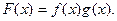
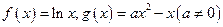 .
.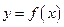 与
与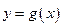 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数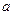 的值并求点P的坐标;(2)若函数
的值并求点P的坐标;(2)若函数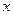 轴的垂线分别与
轴的垂线分别与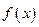 的图像和
的图像和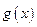 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作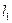 ,以T为切点作
,以T为切点作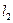 .是否存在实数
.是否存在实数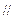
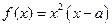 .
.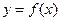 在点
在点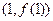 处的切线
处的切线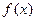 在区间[0,2]上的最大值。
在区间[0,2]上的最大值。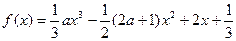 ,
,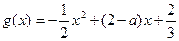
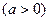 (Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,
(Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,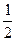 ]内至少存在一实数
]内至少存在一实数 x0使得
x0使得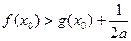 成立,求实数a的取值范围.
成立,求实数a的取值范围.
 ,
, ( )
( )


