题目内容
设数列{an}中,若an+1=an+an+2(n∈N*),则称数列{an}为“凸数列”,已知数列{bn}为“凸数列”,且b1=1,b2=-2,则数列{bn}的前2014项和为________.
-5
由“凸数列”的定义,可知,b1=1,b2=-2,b3=-3,b4=-1,b5=2,b6=3,b7=1,b8=-2,…,故数列{bn}是周期为6的周期数列,又b1+b2+b3+b4+b5+b6=0,故数列{bn}的前2014项和S2014=b1+b2+b3+b4=1-2-3-1=-5.

练习册系列答案
相关题目
 中,
中, ,则
,则 ( )
( )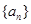 满足
满足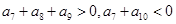 ,则当
,则当 时,
时,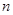 项和最大.
项和最大.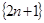 中各项划分为:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33), (35,37,39,41)。照此下去,第100个括号里各数的和为
中各项划分为:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33), (35,37,39,41)。照此下去,第100个括号里各数的和为 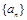 中,
中,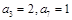 ,若数列
,若数列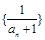 为等差数列,则
为等差数列,则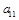 =( )
=( )

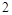
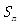 ,若
,若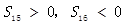 ,则在
,则在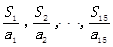 中最大的是( )
中最大的是( ) 


