ћвƒњƒЏ»Ё
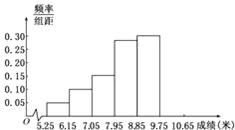
°Њћвƒњ°њƒ≥ –ќ™ЅЋЅЋљвљсƒкЄя÷–±ѕ“µ…ъµƒћеƒ№„іњц£ђі”±Њ –ƒ≥–£Єя÷–±ѕ“µ∞а÷–≥й»°“їЄц∞аљш––«¶«т≤в ‘£ђ≥…Љ®‘Џ8.0√„£®ЊЂ»Јµљ0.1√„£©“‘…ѕµƒќ™ЇѕЄс£Ѓ∞—Ћщµ√ эЊЁљш––’ыјнЇу£ђЈ÷≥…6„йї≠≥ц∆µ¬ Ј÷≤Љ÷±ЈљЌЉµƒ“ї≤њЈ÷£®»зЌЉ£©£ђ“—÷™і”„уµљ”“«∞5Єц–°„йµƒ∆µ¬ Ј÷±рќ™0.04£ђ0.10£ђ0.14£ђ0.28£ђ0.30£ЃµЏ6–°„йµƒ∆µ э «7£Ѓ
£®1£©«у’віќ«¶«т≤в ‘≥…Љ®ЇѕЄсµƒ»Ћ э£ї
£®2£©»ф”…÷±ЈљЌЉјієјЉ∆’в„й эЊЁµƒ÷–ќї э£ђ÷Є≥цЋь‘ЏµЏЉЄ„йƒЏ£ђ≤ҐЋµ√чјн”…£ї
£®3£©»ф≤ќЉ”іЋіќ≤в ‘µƒ—І…ъ÷–£ђ”–9»Ћµƒ≥…Љ®ќ™”≈–г£ђѕ÷‘Џ“™і”≥…Љ®”≈–гµƒ—І…ъ÷–£ђЋжїъ—°≥ц2»Ћ≤ќЉ”°∞±ѕ“µ‘Ћґѓїб°±£ђ“—÷™a°Ґbµƒ≥…Љ®Њщќ™”≈–г£ђ«уЅљ»Ћ÷Ѕ…ў”–1»Ћ»л—°µƒЄ≈¬ °£
°Њір∞Є°њ£®1£©36£®2£©4£®3£©![]()
°Њљвќц°њ ‘ћвЈ÷ќц£Ї£®1£©”…∆µ¬ Ј÷≤Љ÷±ЈљЌЉµƒ√жїэЇЌќ™1£ђњ…«уµ√µЏ6„й∆µ¬ ќ™0.14,і”ґш«уµ√„№»Ћ эќ™50»Ћ£ђ”…ЌЉњ…÷™µЏ4°Ґ5°Ґ6„й≥…Љ®ЊщЇѕЄс£ђ”…∆µ¬ ЇЌ≥Ћ“‘„№»Ћ эњ…«у°££®2£©÷±ЈљЌЉ÷–ќї э‘Џ√жїэќ™0.5µƒќї÷√£ђ«∞»э„йµƒ∆µ¬ ЇЌќ™0.28£ђ«∞Ћƒ„йµƒ∆µ¬ ЇЌќ™0.56£ђЋщ“‘÷–ќї эќї”ЏµЏ4„йƒЏ°££®3£©…и≥…Љ®”≈–гµƒ9»ЋЈ÷±рќ™a£ђb£ђc£ђd£ђe£ђf£ђg£ђh£ђk£ђ≤…”√√ґЊўЈ®£ђЋг≥ц„№«йњц36÷÷£ђЇЌ¬ъ„гћхЉюµƒ«йњцє≤15÷÷£ђ”…є≈µдЄ≈–Ќњ…«уµ√Є≈¬ °£
‘ћвљвќц£Ї£®1£©µЏ6–°„йµƒ∆µ¬ ќ™1©Б£®0.04+0.10+0.14+0.28+0.30£©=0.14£ђ
°аіЋіќ≤в ‘„№»Ћ эќ™![]() £®»Ћ£©£Ѓ
£®»Ћ£©£Ѓ
°аµЏ4°Ґ5°Ґ6„й≥…Љ®ЊщЇѕЄс£ђ»Ћ эќ™£®0.28+0.30+0.14£©°Ѕ50=36£®»Ћ£©£Ѓ
£®2£©÷±ЈљЌЉ÷–÷–ќї эЅљ≤аµƒ√жїэѕаµ»£ђЉі∆µ¬ ѕаµ»£Ѓ«∞»э„йµƒ∆µ¬ ЇЌќ™0.28£ђ«∞Ћƒ„йµƒ∆µ¬ ЇЌќ™0.56£ђ°а÷–ќї эќї”ЏµЏ4„йƒЏ£Ѓ
£®3£©…и≥…Љ®”≈–гµƒ9»ЋЈ÷±рќ™a£ђb£ђc£ђd£ђe£ђf£ђg£ђh£ђk£ђ
‘т—°≥цµƒ2»ЋЋщ”–њ…ƒ№µƒ«йњцќ™£Їab£ђac£ђad£ђae£ђaf£ђag£ђah£ђak£їbc£ђbd£ђbe£ђbf£ђ
bg£ђbh£ђbk£їcd£ђce£ђcf£ђcg£ђch£ђck£їde£ђdf£ђdg£ђdh£ђdk£їef£ђeg£ђeh£ђek£їfg£ђfh£ђfk£їgh£ђgk£їhk£Ѓє≤36÷÷£ђ∆д÷–a°Ґbµљ…ў”–1»Ћ»л—°µƒ«йњц”–15÷÷£ђ
°аa°ҐbЅљ»Ћ÷Ѕ…ў”–1»Ћ»л—°µƒЄ≈¬ ќ™![]() £Ѓ
£Ѓ

°Њћвƒњ°њƒ≥єЂЋЊљсƒк“ї‘¬ЈЁЌ∆≥ц–¬≤ъ∆ЈA£ђ∆д≥…±ЊЉџќ™492‘™/Љю£ђЊ≠ ‘ѕъµч≤й£ђѕъ џЅњ”лѕъ џЉџµƒєЎѕµ»зѕ¬±н£Ї
ѕъ џЉџ£®x/‘™Љю£© | 650 | 662 | 720 | 800 |
ѕъ џЅњ£®yЉю£© | 350 | 333 | 281 | 200 |
”…іЋњ…÷™£ђѕъ џЅњy£®Љю£©”лѕъ џЉџx£®‘™/Љю£©њ…љьЋ∆њі„ч“їіќЇѓ эy=kx+bµƒєЎѕµ£®Ќ®≥£»°±н÷–ѕаЊаљѕ‘ґµƒЅљ„й эЊЁЋщµ√“їіќЇѓ эљѕќ™ЊЂ»Ј£©£Ѓ
£®1£©–і≥ц“‘xќ™„‘±дЅњµƒЇѓ эyµƒљвќц љЉ∞ґ®“е”т£ї
£®2£© ‘ќ £Їѕъ џЉџґ®ќ™ґа…ў ±£ђ“ї‘¬ЈЁѕъ џјы»у„оіу£њ≤Ґ«у„оіуѕъ џјы»уЇЌіЋ ±µƒѕъ џЅњ£Ѓ
°Њћвƒњ°њƒ≥єЂЋЊќ™»Јґ®ѕ¬“їƒкґ»Ќґ»лƒ≥÷÷≤ъ∆Јµƒ–ыіЂЈ—,–иЅЋљвƒк–ыіЂЈ—x£®µ•ќї:«І‘™£©ґ‘ƒкѕъ џЅњy£®µ•ќї:t£©ЇЌƒкјы»уz£®µ•ќї:«І‘™£©µƒ”∞ѕм.ґ‘љь8ƒкµƒƒк–ыіЂЈ—xiЇЌƒкѕъ џЅњyi£®i£љ1,2,°≠,8£© эЊЁ„чЅЋ≥х≤љі¶јн£ђµ√µљѕ¬√жµƒ…ҐµгЌЉЉ∞ѕ¬√ж“ї–©Ќ≥Љ∆Ѕњµƒ÷µ.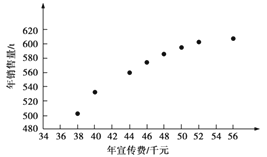
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
±н÷– ![]() ,
, ![]() .
.
Єљ£Їґ‘”Џ“ї„й эЊЁ£®u1,v1£©,£®u2,v2£©,°≠,£®un,vn£©,∆дїЎєй÷±ѕяv£љ¶Ѕ£Ђ¶¬uµƒ–±¬ ЇЌљЎЊаµƒ„оѕ¬ґю≥ЋєјЉ∆Ј÷±рќ™ 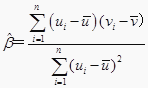 ,
, ![]() .
.
£®1£©ЄщЊЁ…ҐµгЌЉ≈–ґѕ,y£љa£Ђbx”л ![]() ƒƒ“їЄц “Ћ„чќ™ƒкѕъ џЅњyєЎ”Џƒк–ыіЂЈ—xµƒїЎєйЈљ≥ћја–Ќ£њ£®Єш≥ц≈–ґѕЉіњ…,≤ї±ЎЋµ√чјн”…£©
ƒƒ“їЄц “Ћ„чќ™ƒкѕъ џЅњyєЎ”Џƒк–ыіЂЈ—xµƒїЎєйЈљ≥ћја–Ќ£њ£®Єш≥ц≈–ґѕЉіњ…,≤ї±ЎЋµ√чјн”…£©
£®2£©ЄщЊЁ£®1£©µƒ≈–ґѕљбєыЉ∞±н÷– эЊЁ,љ®ЅҐyєЎ”ЏxµƒїЎєйЈљ≥ћ£ї
£®3£©“—÷™’в÷÷≤ъ∆Јµƒƒкјы»уz”лx,yµƒєЎѕµќ™z£љ0.2y£≠x.ЄщЊЁ£®2£©µƒљбєыїЎірѕ¬Ѕ–ќ ћв£Ї
Ґўƒк–ыіЂЈ—x£љ49 ±,ƒкѕъ џЅњЉ∞ƒкјы»уµƒ‘§±®÷µ ±ґа…ў£њ
ҐЏƒк–ыіЂЈ—xќ™Їќ÷µ ±,ƒкјы»уµƒ‘§±®÷µ„оіу£њ