题目内容
【题目】若函数f（x）是偶函数，且在（﹣∞，0]上是增函数，又f（2）=0，则xf（x）＞0的解集是（ ）
A.（﹣2，2）
B.（﹣∞，﹣2）∪（0，2）
C.（﹣∞，﹣2）∪（2，+∞）
D.（﹣2，0]∪（2，+∞）
【答案】B
【解析】解：∵偶函数f（x）在（﹣∞，0]上为增函数，又f（﹣2）=0，
∴函数f（x）在（0，+∞）上为减函数，且f（﹣2）=f（2）=0，
画出函数f（x）的示意图如图所示：
∵不等式xf（x）＞0等价为 
或 
，
∴由图得，0＜x＜2或x＜﹣2，
∴不等式的解集是（﹣∞，﹣2）∪（0，2），
故选：B．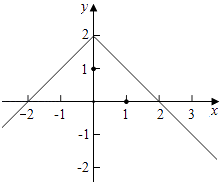
【考点精析】认真审题，首先需要了解奇偶性与单调性的综合(奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性)．
练习册系列答案
相关题目
