题目内容
已知点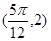 在函数
在函数 的图象上,直线
的图象上,直线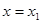 、
、 是
是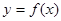 图象的任意两条对称轴,且
图象的任意两条对称轴,且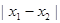 的最小值为
的最小值为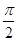 .
.
(1)求函数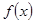 的单递增区间和其图象的对称中心坐标;
的单递增区间和其图象的对称中心坐标;
(2)设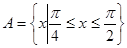 ,
,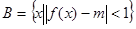 ,若
,若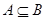 ,求实数
,求实数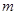 的取值范围.
的取值范围.
(1)函数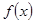 的单递增区间为
的单递增区间为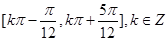 ,图象的对称中心坐标
,图象的对称中心坐标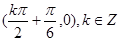 ;(2)实数
;(2)实数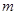 的取值范围
的取值范围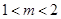 .
.
解析试题分析:(1)先根据点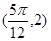 在函数上,
在函数上,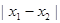 的最小值为
的最小值为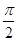 求出
求出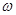 、
、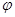 ,再根据
,再根据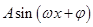 的性质求解即可;(2)由
的性质求解即可;(2)由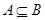 知,当
知,当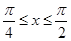 时
时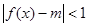 恒成立,即
恒成立,即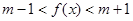 恒成立,所以
恒成立,所以 ,解出
,解出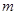 的取值范围即可.
的取值范围即可.
试题解析:(1)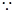
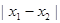 的最小值为
的最小值为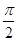 ,
,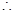 周期
周期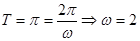
又图象经过点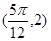 ,
,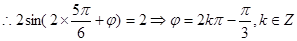
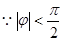 ,
,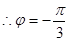
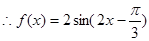 3分
3分
单调递增区间为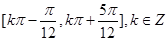 5分
5分
对称中心坐标为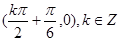 . 7分
. 7分
(2)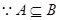 ,
,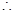 当
当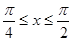 时
时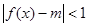 恒成立
恒成立
即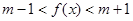 恒成立
恒成立
即 ,
,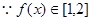 ,
,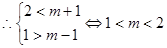 . 14分
. 14分
考点:三角函数解析式的求法、三角函数的图象和性质.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 )的周期为π,且图象上一个最低点为M
)的周期为π,且图象上一个最低点为M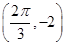 .
. 时,求f(x)的最值.
时,求f(x)的最值.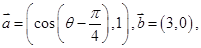 其中
其中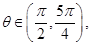 若
若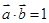 .
.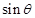 的值;
的值;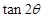 的值.
的值. 的部分图像如图所示.
的部分图像如图所示.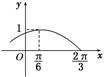
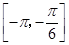 时,求f(x)的取值范围.
时,求f(x)的取值范围. .
.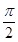 )的部分图象如图所示.
)的部分图象如图所示.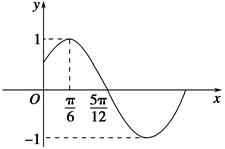
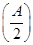 的取值范围.
的取值范围. 中,角A,B,C所对的边分别为a,b,c,已知
中,角A,B,C所对的边分别为a,b,c,已知 .
. ,且
,且 时,求a的值;
时,求a的值; 时,求
时,求 的值.
的值. ,
,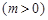 的最大值为2.
的最大值为2.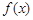 在
在 上的值域;
上的值域; 外接圆半径
外接圆半径 ,
, ,角
,角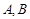 所对的边分别是
所对的边分别是 ,求
,求 的值.
的值.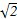 )(x≠0),且cosα=
)(x≠0),且cosα=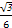 x.求sinα+
x.求sinα+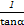 的值.
的值.