题目内容
已知函数 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
解析试题分析:(Ⅰ)可直接将角代入求值,也可先用正弦、余弦二倍角公式和化一公式将此函数化简为正弦型函数,再代入角求值。(Ⅱ)根据 的范围先求整体角的范围,再根据三角函数图像求其值域。
的范围先求整体角的范围,再根据三角函数图像求其值域。
试题解析:解:(Ⅰ)由
 ,
,
得 .
.
所以 . 8分
. 8分
(Ⅱ)因为 ,
,
所以 .
.
当 ,即
,即 时,
时,
函数 在区间
在区间 上的最大值为
上的最大值为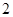 .
.
当 ,即
,即 时,
时,
函数 在
在 上的最小值为
上的最小值为 . 13分
. 13分
考点:用二倍角公式、化一公式化简三角函数,考查三角函数图像。

练习册系列答案
相关题目
 .
. ,
, ,
, 分别是
分别是 的三个内角
的三个内角 ,
, ,
, 所对的边,且
所对的边,且 .
. ,
, ,求
,求 .
.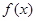 的最小正周期和图像的对称轴方程;
的最小正周期和图像的对称轴方程; 上的值域.
上的值域. ,
,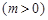 的最大值为2.
的最大值为2.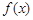 在
在 上的值域;
上的值域; 外接圆半径
外接圆半径 ,
, ,角
,角 所对的边分别是
所对的边分别是 ,求
,求 的值.
的值.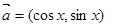 ,
, ,函数
,函数 。
。 的值域和函数的单调递增区间;
的值域和函数的单调递增区间;  ,且
,且 时,求
时,求 的值.
的值. ,记函数
,记函数 的最小正周期为
的最小正周期为 ,向量
,向量 ,
, (
( ),且
),且 .
. 在区间
在区间 上的最值;
上的最值; 的值.
的值. ;
; 为第二象限角,化简
为第二象限角,化简 .
. 为钝角的的三角形
为钝角的的三角形 内角
内角 的对边分别为
的对边分别为 、
、 、
、 ,
, ,且
,且 与
与 垂直.
垂直. 的取值范围
的取值范围